How to Add 3 Digit Numbers Using Place Value Method with Solved Examples
Three-digit addition is the process of adding two or more three-digit numbers. The two numbers' total is the name given to the outcome. There are two techniques to add three digits: addition with regrouping, sometimes known as the carrying forward approach, and addition without regrouping.
An added and an augend are combined to find a total. The addend is sometimes referred to as an addend. The term total can also be referred to as the sum. We will discuss 3-digit addition without carrying today.
What is Addition?
There are four basic operations of arithmetic, i.e., addition, subtraction, multiplication, and division. Today, we will discuss addition or, to be more precise, three-digit addition without carrying. The addition is the process of adding two or more numbers together, and the result obtained is known as the sum of the given numbers. Every arithmetic operation has its unique symbol. In addition, the symbol is ‘+’.
Arithmetic Operations
3 Digit Addition
In addition to 3 digits, the place value of the numbers is given more importance. The place value is expressed here as ones, tens, and hundreds. To add 3 digits numbers, arrange them column-wise according to their place values. Digits are added one by one. The numbers added are called addends, and the answer obtained is known as their sum.
3 digit addition can be done in two ways. First is the ‘regrouping’ method, also known as carrying forward, and the ‘without regrouping’ method, also known as no carrying forward.
3 Digits Addition with Carry Forward Method
Types of Addition
1. Addition of 3 Digit Numbers with Regrouping:
There is a condition in the ‘regrouping’ method, also known as the carrying forward method. Here, we have to move the extra number to the next column if the sum of the numbers in either of the columns is more than 9. We begin from the one's column and move left towards the tens and hundreds of columns.
Let us take an addition of 3 digits of the addition of 528 and 298.
$528 + 298$
If we start adding from one’s column, we get $8{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}16$, with 1 as the carrying number.
The tens column already has a carrying number, so $2{\rm{ }} + {\rm{ }}9{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}12$ with 1 as the carrying number.
The hundreds column already has a carrying number, so we get $5{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}8$.
Therefore, the result is 826.
This example can be declared as 3 digit number addition with regrouping.
2. Addition of 3 Digit Numbers without Regrouping:
The ‘Without regrouping’ method is very simple, also known as the carrying forward method. It is used in our day-to-day lifestyle, like shopping and any transaction. Here, when the sum is less than or equal to 9, we write the number according to its place value column, which does not carry forward any number.
Let us take an addition of 3 digits of the addition of 558 and 231.
$558 + 231$
If we start adding from one’s column, we get $8{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}9$, and no extra carry number.
For the tens column, we get $5{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}8$ and no extra carry number.
For the hundreds column, we get $5{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}7$ with no extra carry number.
Therefore, the result is 789.
This example can be declared as 3-digit addition numbers without regrouping.
3 Digit Addition Worksheets
Now, let us solve some 3-digit addition with carry-over examples or 3 Digit Addition with carry-over worksheets given below:
Example 1:
Add the 3-digit numbers: 232 and 172.
Solution:
First, we will have to add the digits of the one's column, then the tens and then the hundreds. So, let us get started.
$232 + 172$
Numbers in the ones columns: $2{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}4$.
As the sum of the one's columns is less than 9, we do not have a carry-over number.
Numbers in the tens columns: $3{\rm{ }} + {\rm{ }}7{\rm{ }} = {\rm{ }}10$.
As the sum of the tens columns is more than 9, we have a carry-over number of 1.
Numbers in the hundreds columns along with the carry over number: $2{\rm{ }} + {\rm{ }}1{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}4$.
Therefore, the result we obtained is $232{\rm{ }} + {\rm{ }}172{\rm{ }} = {\rm{ }}404$.
Example 2:
Add the 3-digit numbers: 511 and 109.
Solution:
First, we will have to add the digits of the one's column, then the tens and then the hundreds. So, let us get started.
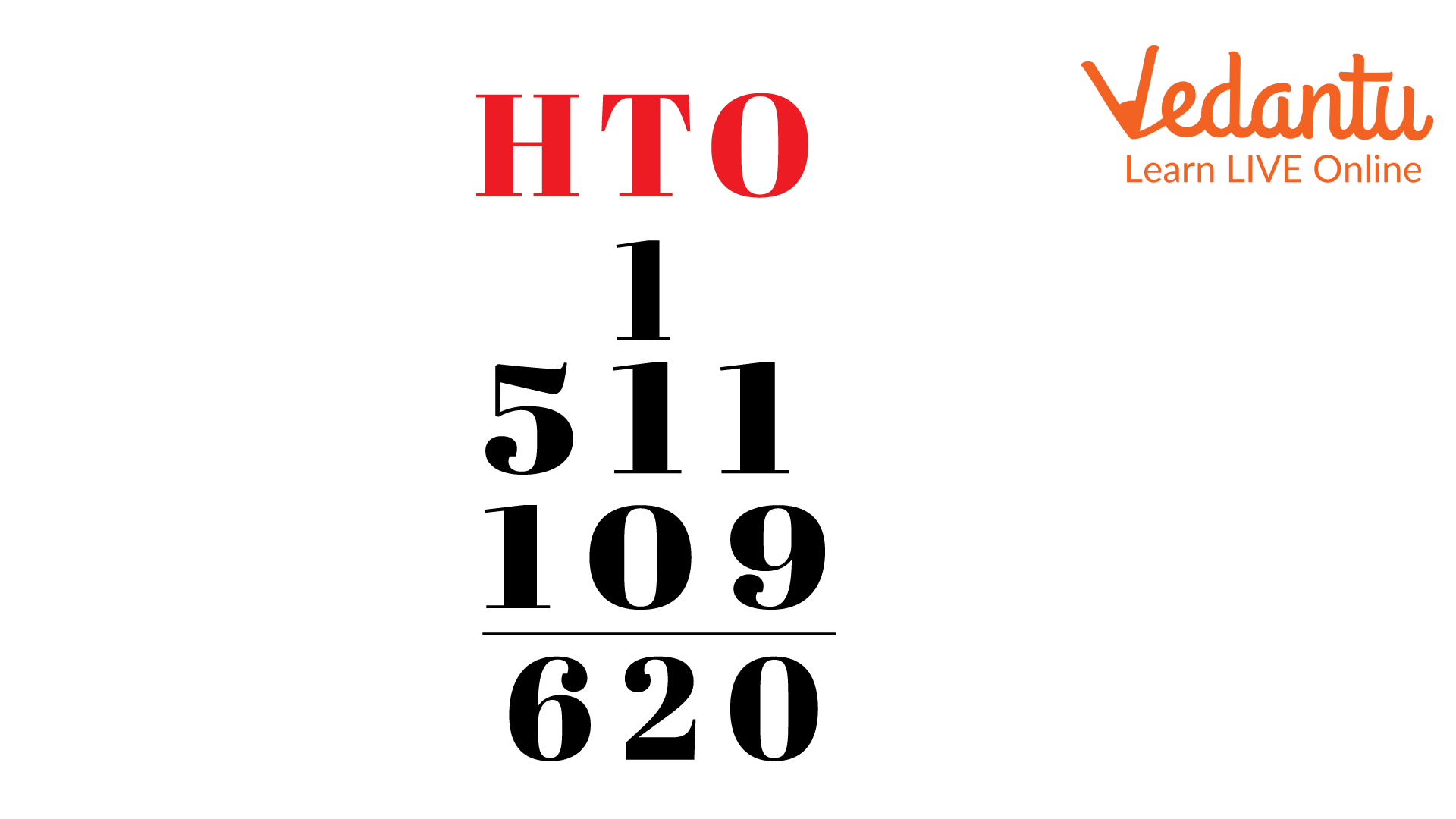
$511 + 109$
Numbers in the ones columns: $1{\rm{ }} + {\rm{ }}9{\rm{ }} = {\rm{ }}10$.
As the sum of the one’s columns is more than 9, we have a carry-over number of 1.
Numbers in the tens columns along with the carry over number: $1{\rm{ }} + {\rm{ }}0{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}2$.
As the sum of the one's columns is less than 9, we do not have a carry-over number.
Numbers in the hundreds columns: $5{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}6$.
Therefore, the result we obtained is $511{\rm{ }} + {\rm{ }}109{\rm{ }} = {\rm{ }}620$.
Example 3:
Perform addition of $228{\rm{ }} + {\rm{ }}228$.
Solution:
First, we will have to add the digits of the one's column, then the tens and then the hundreds. So, let us get started.
$228 + 228$
Numbers in the ones columns: $8{\rm{ }} + {\rm{ }}8{\rm{ }} = {\rm{ }}16$.
As the sum of the one’s columns is more than 9, we have a carry-over number of 1.
Numbers in the tens columns along with the carry-over number: $2{\rm{ }} + {\rm{ }}2{\rm{ }} + {\rm{ }}1{\rm{ }} = {\rm{ }}5$.
As the sum of the one's columns is less than 9, we do not have a carry-over number.
Numbers in the hundreds columns: $2{\rm{ }} + {\rm{ }}2{\rm{ }} = {\rm{ }}4$.
Therefore, the result we obtained is $228{\rm{ }} + {\rm{ }}228{\rm{ }} = {\rm{ }}456$.
Conclusion
The addition is one of the four basic operations of Mathematics, with the other three being subtraction, multiplication, and division. The addition means finding the total or sum by combining two or more numbers. If the addition of the digits is more than 9 in each column, it is termed as addition with regrouping. And If the addition of the digits is less than 9 in each column, it is termed as an addition without regrouping.
FAQs on Addition of 3 Digit Numbers with Regrouping and Without Regrouping
1. What is addition of 3 digit numbers?
The addition of 3 digit numbers is the process of finding the total when two or more numbers between 100 and 999 are added together. In this method, digits are added according to their place values — ones, tens, and hundreds. For example, 245 + 312 = 557, where each column (ones, tens, hundreds) is added separately.
2. How do you add two 3 digit numbers step by step?
To add two 3 digit numbers, align them by place value and add column by column from right to left.
- Step 1: Write the numbers vertically according to place value (ones under ones, tens under tens, hundreds under hundreds).
- Step 2: Add the ones digits.
- Step 3: Add the tens digits (including any carry).
- Step 4: Add the hundreds digits (including any carry).
Example: 456 + 123 = 579.
3. How do you add 3 digit numbers with carrying?
When adding 3 digit numbers with carrying, you regroup when the sum of a column is 10 or more.
- Add the ones digits. If the sum is 10 or more, write the ones digit and carry the tens digit to the next column.
- Add the tens digits plus any carry.
- Add the hundreds digits plus any carry.
Example: 278 + 145 = 423 (8 + 5 = 13, write 3 carry 1).
4. How do you add three 3 digit numbers?
To add three 3 digit numbers, align all numbers by place value and add each column from right to left.
- Write the numbers vertically.
- Add all ones digits and carry if needed.
- Add all tens digits and include any carry.
- Add all hundreds digits and include any carry.
Example: 123 + 245 + 111 = 479.
5. What is the place value method in addition of 3 digit numbers?
The place value method in addition means adding digits according to their ones, tens, and hundreds positions. Each digit is added within its correct column. For example, in 362 + 415:
- Ones: 2 + 5 = 7
- Tens: 6 + 1 = 7
- Hundreds: 3 + 4 = 7
So, the sum is 777.
6. Can you give an example of addition of 3 digit numbers with regrouping?
Yes, addition of 3 digit numbers with regrouping involves carrying over when a column sum exceeds 9.
- Example: 487 + 256
- Ones: 7 + 6 = 13 (write 3, carry 1)
- Tens: 8 + 5 + 1 = 14 (write 4, carry 1)
- Hundreds: 4 + 2 + 1 = 7
The final answer is 743.
7. What are common mistakes when adding 3 digit numbers?
Common mistakes in adding 3 digit numbers include misalignment of digits and forgetting to carry.
- Not lining up numbers by place value.
- Forgetting to add the carry to the next column.
- Adding digits in the wrong order.
- Skipping a column during calculation.
Careful column alignment helps avoid these errors.
8. What is the expanded form method for adding 3 digit numbers?
The expanded form method adds 3 digit numbers by breaking them into hundreds, tens, and ones before adding.
- Example: 324 = 300 + 20 + 4
- 215 = 200 + 10 + 5
- Add: (300+200) + (20+10) + (4+5)
This gives 500 + 30 + 9 = 539.
9. How do you check the answer after adding 3 digit numbers?
You can check addition of 3 digit numbers by using the inverse operation, which is subtraction.
- If 468 + 231 = 699
- Check by subtracting: 699 − 231 = 468
If the result matches the original number, the addition is correct.
10. Why is place value important in addition of 3 digit numbers?
Place value is important in addition of 3 digit numbers because each digit represents a different value based on its position. The hundreds, tens, and ones columns must be added separately to get the correct total. For example, in 345, the digit 3 represents 300, not 3. Correct place value alignment ensures accurate results.
