




Step-by-Step Techniques to Add Without a Number Line
The addition between the integers is not completely similar to the addition of natural numbers. At times, when we are asked to add we may have to do subtraction between the given numbers to obtain the result. In case of integer addition, when one of the two integers is negative and the other one is positive in such cases we subtract the numbers and give the sign of the greater number to the result. When the integers carry the same sign, be it positive or negative, we add the integers and give the common sign to the result.
What are Integers?
The Latin term "Integer," which implies entire or whole, is where the word "integer" first appeared. A particular category of numbers called integers includes zero, positive numbers, and negative numbers. Symbol ‘Z’ is generally used to denote integers. Integers are generally represented on a number line. Zero is generally considered as the center of the number line and is neither negative nor positive. The negative numbers are generally placed to the left of zero on the number line while the positive numbers are placed on the right side of 0.
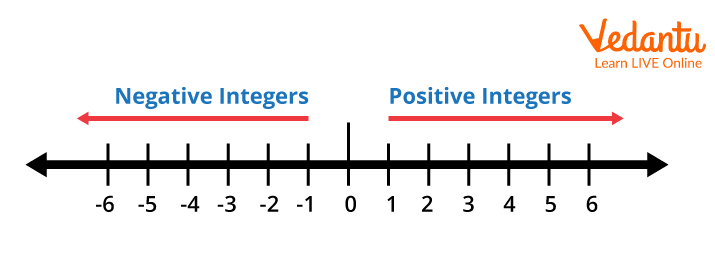
Number Line
Addition of Integers Without Using Number Line
In addition of integers without using a number line, we generally follow basic addition and also subtraction which depends upon the signs of the given integers. Further, we will see the rules of addition of integers without using the number line and thus perform addition between the integers easily and efficiently.
Rules for Addition of Integers (Without Using Number Line) :
If a positive integer is added to a positive integer, both the integers will be added and a positive sign will be attached to the result obtained.
Example :
Add \[( + 7)\] and \[( + 3)\]\[ = 7 + 3 = 10\] i.e \[ + 10\]
Add \[( + 4)\] and \[( + 8)\]\[ = 4 + 8 = 12\] i.e \[ + 12\]
If a negative integer is added to a negative integer, both the numbers will be added and a negative sign will be attached to the result obtained.
Example :
Add \[( - 3)\] and \[( - 7)\]\[ = (-3) + (-7) = (-10)\] i.e \[ - 10\]
Add \[( - 4)\] and \[( - 8)\]\[ = (-4) + (-8) = (-12)\] i.e \[ - 12\]
If a positive integer is added to a negative integer, the smaller one among them will be subtracted from the one which is greater and the sign of the greater integer will be attached to the result obtained.
Example :
Add \[( +7)\] and \[( - 3)\]
Here, 7 is greater and 3 is smaller. Therefore, \[ 7 - 3 = 4\]
The sign of the greater number is positive so the result will also be positive i.e.\[ + 4\]
Add \[( +3)\] and \[( - 8)\]
Here, 8 is greater and 3 is smaller. Therefore, \[ 8 - 3 = 5\]
The sign of the greater number is negative so the result will also be negative i.e.\[ - 5\]
Solved Examples :
Evaluate : \[( - 4)+( - 5)\]
Solution : Here, as we can observe that the integers to be added have the same sign i.e both the integers are negative .
So, as per the rules for addition, we add them and the common sign is attached to the result.
Therefore, \[(- 4)+ ( -5)= -( 4 + 5) = - 9\]
Evaluate : \[(- 13) + (+ 17)\]
Solution : Here, as we can observe that the integers to be added have the opposite sign i.e. one is negative and the other is positive .
So, as per the rules for addition, we subtract the smaller number from the greater one and then the sign of the greater integer is attached to the result.
Here, 17 is the greater number.
So, \[17 - 13 = 4\]
As the greater number is positive, the result will also be positive.
Therefore, \[(- 13) + (+ 17)= + 4\]
Evaluate : \[(+ 14) + (+ 15)\]
Solution : Here, as we can observe that the integers to be added have the same sign i.e both the integers are positive .
So, as per the rules for addition, we add them and the common sign is attached to the result.
Therefore,\[(+ 14)+ ( +15)= 14 + 15 = 29\]
Conclusion :
Thus, we can observe that while adding the integers manually without using a number line, we generally add the ones with common sign and give the common sign to the result obtained. In case of opposite signs, we subtract the smaller one from the greater one and the sign of the greater one is attached to the result obtained.
FAQs on Add Without Using a Number Line: Easy Strategies Explained
1. What are the basic rules for adding integers without using a number line?
To add integers without a number line, you can follow two simple rules based on their signs:
Same Signs: If both integers are positive or both are negative, add their values and keep the common sign. For example, (-5) + (-3) = -8.
Different Signs: If one integer is positive and the other is negative, subtract the smaller absolute value from the larger absolute value. The result takes the sign of the integer with the larger absolute value. For example, to solve 10 + (-4), you subtract 4 from 10 to get 6, and since 10 is larger and positive, the answer is +6.
2. When is it better to add integers without using a number line?
While a number line is useful for visualising addition with small numbers, it becomes impractical for large numbers. For example, adding 250 + (-175) would require a very long number line. Learning the rules for adding integers is a more efficient and essential strategy for solving problems with larger numbers quickly and accurately.
3. How can you add integers in a real-world scenario, for example, with money?
You can think of adding integers in terms of money. A positive number is money you have, and a negative number is money you owe or spend. If you have ₹100 (+100) in your wallet and you spend ₹30 (-30), you add them together: 100 + (-30). Since the signs are different, you subtract 30 from 100, which leaves you with ₹70. This is a practical example of adding integers without needing a number line.
4. Why do we subtract when adding a positive and a negative integer?
We subtract when adding a positive and a negative integer because they represent opposite effects that partially cancel each other out. Think of it as taking steps in opposite directions. If you take 8 steps forward (+8) and 5 steps backward (-5), you don't end up 13 steps away. The 5 steps backward cancel out 5 of the steps forward. Your final position is the difference between the two, which is 8 - 5 = 3 steps forward from where you started.
5. What is an 'additive inverse' and how does it simplify addition?
The additive inverse of a number is the same number but with the opposite sign. For example, the additive inverse of 9 is -9, and the additive inverse of -25 is 25. This concept is very useful because the sum of any integer and its additive inverse is always zero. This can simplify problems like 42 + (-15) + (-42). You can immediately see that 42 and -42 are additive inverses, so they add up to zero, leaving just -15 as the answer.
6. What happens when zero is added to any negative integer?
When zero is added to any integer, whether positive or negative, the integer's value does not change. Zero is known as the additive identity. For example, if you add zero to -12, the result remains -12, just as 12 + 0 = 12. So, (-12) + 0 = -12.
7. What is a common mistake when adding two negative integers without a number line?
A common mistake is to see two negative signs and think of subtraction. For example, when faced with (-7) + (-5), some students might incorrectly subtract 5 from 7. The correct method is to recognise that the signs are the same, so you must add the absolute values (7 + 5 = 12) and keep the common negative sign, making the correct answer -12.

















