Depreciation Accounting Sale of a Part of Asset

Assets must be removed from the financial records as part of the disposal process. To entirely erase every trace of an asset first from the balance sheet is required (known as derecognition). In the fiscal quarter in which the asset disposal occurs, a gain or loss may need to be recorded on the transaction. We'll assume that the item sold is a fixed asset for the sake of this discussion.

During their valuable lives, one can sell the business's assets at any moment. An asset does not have to be kept until it is destroyed. one must make accounting records about the disposal of an asset. The asset may bring in a profit or a loss when sold. Let's examine the accounting impact of the same.

How to Record the Disposal of Assets?

The basic idea behind asset disposal accounting is to reverse the fixed asset's reported cost and the associated depreciable amount. Any residual discrepancy is recorded as a gain or a loss, depending on how much remains between the two. The net disposal revenues are subtracted from the asset's carrying value to determine the gain or loss.

The choices for recording asset disposal are shown below. From the standpoint of keeping a clean financial statement, thoroughly fixed asset disposal is essential so that the reported balances of capital assets and cumulative depreciation accurately represent the assets that a corporation truly owns.

As part of the disposal procedure, assets must be deleted from the financial records. This is necessary to altogether remove all references to an asset from the balance sheet (known as derecognition). The transaction may require recording a gain or loss in the fiscal quarter in which the asset disposal occurs. For the sake of this discussion, we'll assume that the thing being sold qualifies as a fixed asset.

Record the Disposal of Assets

Loss on Sale of Fixed Assets

A depreciable asset can be sold or disposed of both before and beyond the end of its useful life. Asset disposal may occur during the asset's useful life owing to obsolescence or other circumstances.

The selling revenues from an asset sold after it reaches the end of its useful life should be credited to the asset account. One should record any profit or loss from the sale or disposal of the item in the profit and loss account.

One should assess depreciation for the time the asset is utilized in the year of sale when it is sold while still within its useful life. The provision of depreciation is moved to the asset account in cases when the provision on the depreciation account is maintained.

Loss on Sale of Fixed Assets

Journal Entry for Sale of Assets and Profit on the Sale of Asset

Journal Entry for Profit on the Sale of Asset

Debit all accrued depreciation, credit the fixed asset, and credit the gain on sale of asset account when there is a gain on the sale of a fixed asset. One should also debit cash for the amount received.

For instance, ABC International spends 50,000 dollars on a machine and records $5,000 in depreciation over the subsequent ten years. When the machine completely depreciates at that point, ABC gives it away and makes the following entry.

The number of fixed assets that grow due to an addition or loss on the sale of fixed assets is treated as. The money spent on a fixed asset is considered capital expenditure.

Disposal of assets means the elimination of a long-term asset from the company's accounting records, which is known as the disposal of assets. It is crucial since capital assets are necessary for profitable business operations. Furthermore, keeping up-to-date and accurate accounting records depends on correct accounting of asset disposal. The sale of the asset might be the outcome of numerous things:

• When fully depreciated, an asset needs to be disposed of

• Because an asset is no longer required or helpful, it is sold.

• Unexpected events force the removal of an asset from the books (e.g., theft).

The sale of the asset has an immediate impact on the company's financial statements. In every case, the removal of a capital asset has an impact on the balance sheet.

Additionally, the income statement must show the profit or loss and whether a business sells assets for profit or loss. The loss on the sale of an asset is debited to the profit and loss account

Depreciation on the Sale of Asset

Depreciation is a method used by corporations to divide the cost of fixed assets, such as structures, machinery, equipment, and furnishings, over the years one will use the assets.

The majority of organisations depreciate assets using the straight-line technique for accounting purposes.

Subtract the asset's cost from its salvage value (what you anticipate to be worth at the end of its useful life) to determine depreciation using the straight-line technique. The outcome is the amount that may be depreciated or the depreciable basis. Subtract this sum from the asset's useful life, measured in years. For example, you may calculate the asset's monthly depreciation by dividing by 12.

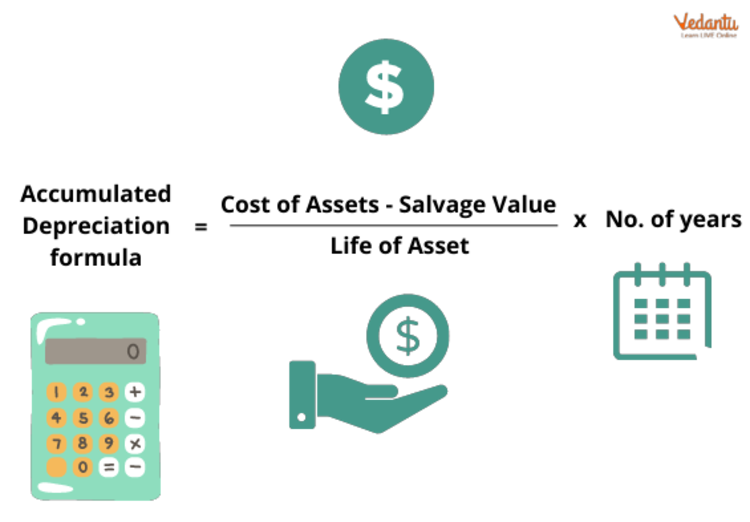
Depreciation on Sale of Assets

Conclusion

Asset disposal includes removing them from the books. This is necessary if an asset is eliminated from the books entirely (known as derecognition). An asset sale may necessitate a gain or loss in the fiscal quarter of the sale. We'll assume the sold item is a fixed asset for this discussion.

Asset disposal accounting involves reversing both the reported cost and accrued depreciation. Any difference is a gain or loss. Net disposal revenues minus the asset's carrying value determines gain or loss.