Understanding Quadrilaterals Class 8 Extra Questions and Answers Free PDF Download
FAQs on CBSE Important Questions for Class 8 Maths Understanding Quadrilaterals - 2025-26
1. What are the most important properties of quadrilaterals I should focus on for my Class 8 Maths exam?
For your Class 8 Maths exam, it's crucial to focus on these key properties:
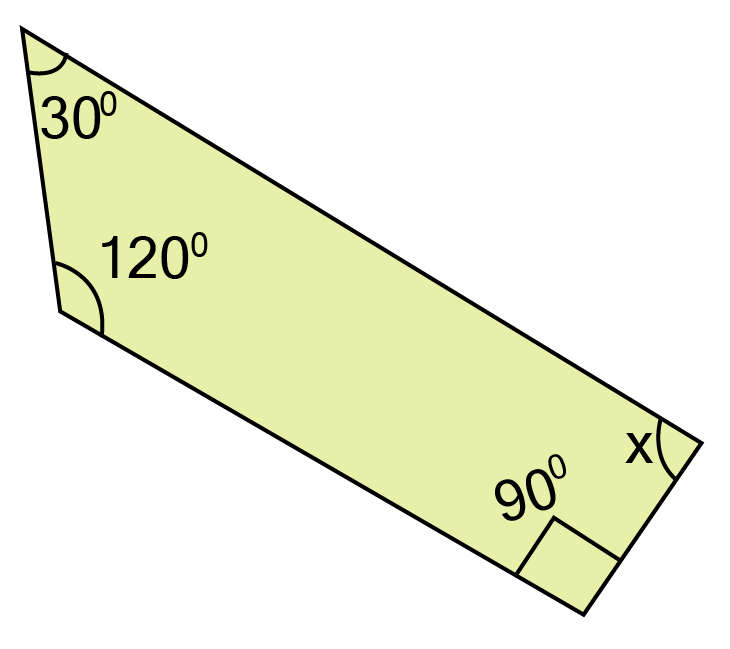
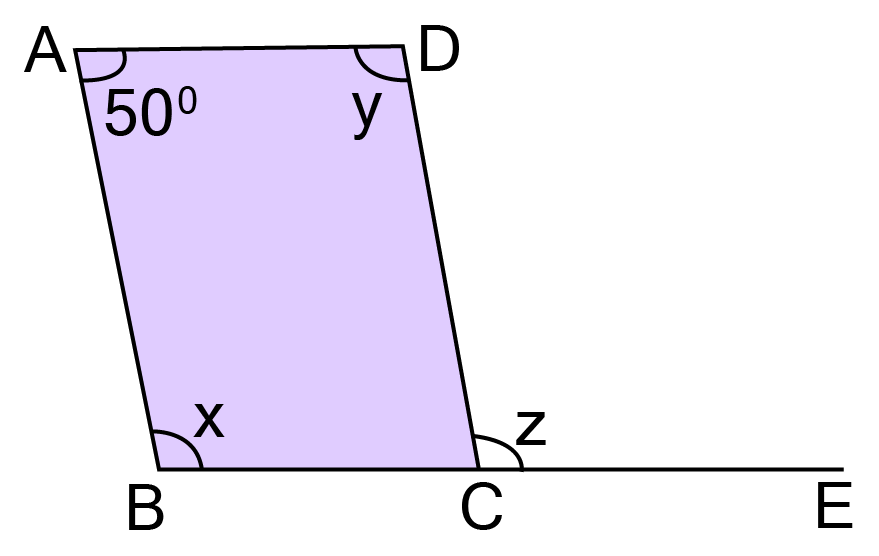
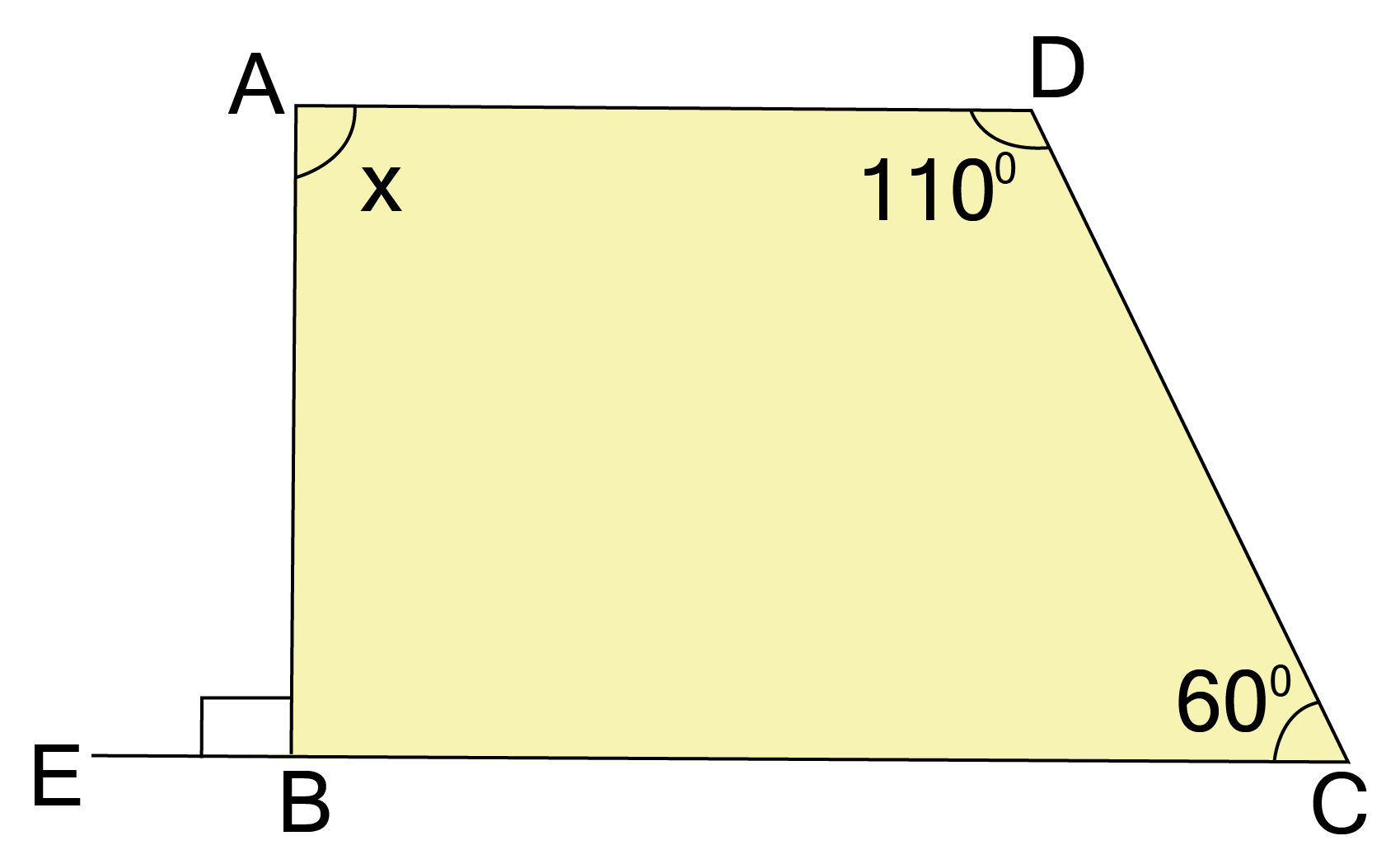
Angle Sum Property: The sum of all interior angles of any quadrilateral is always 360°. This is a fundamental property used in many problems.
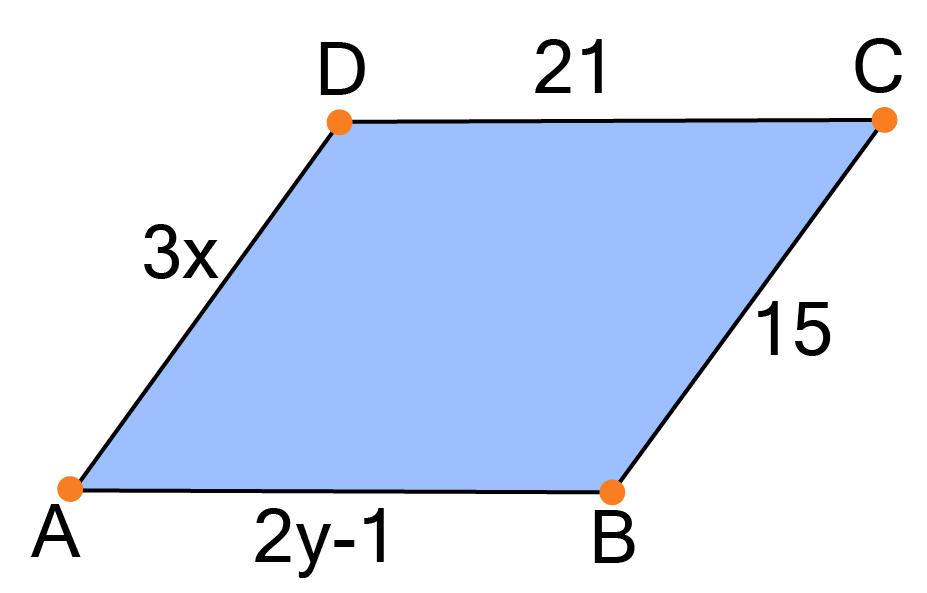
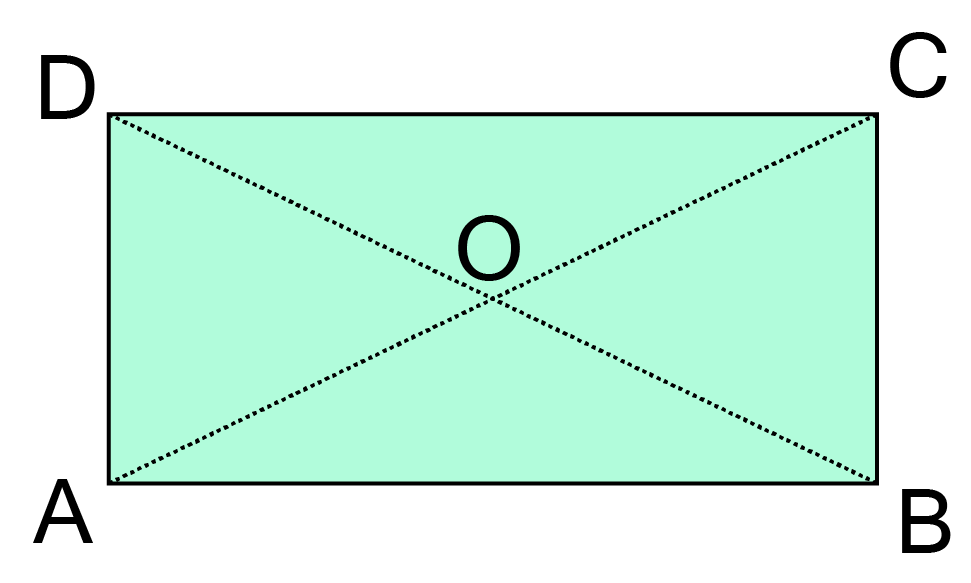
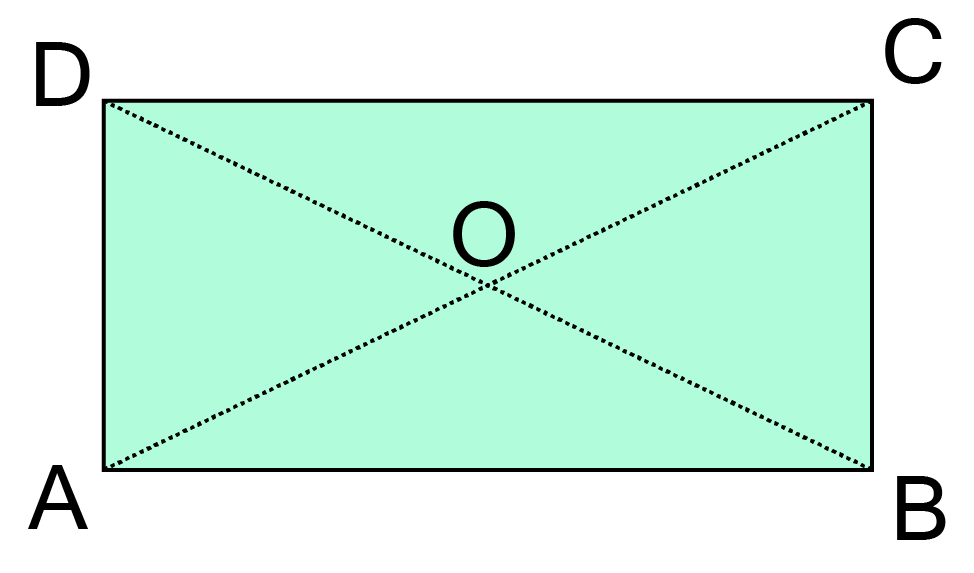
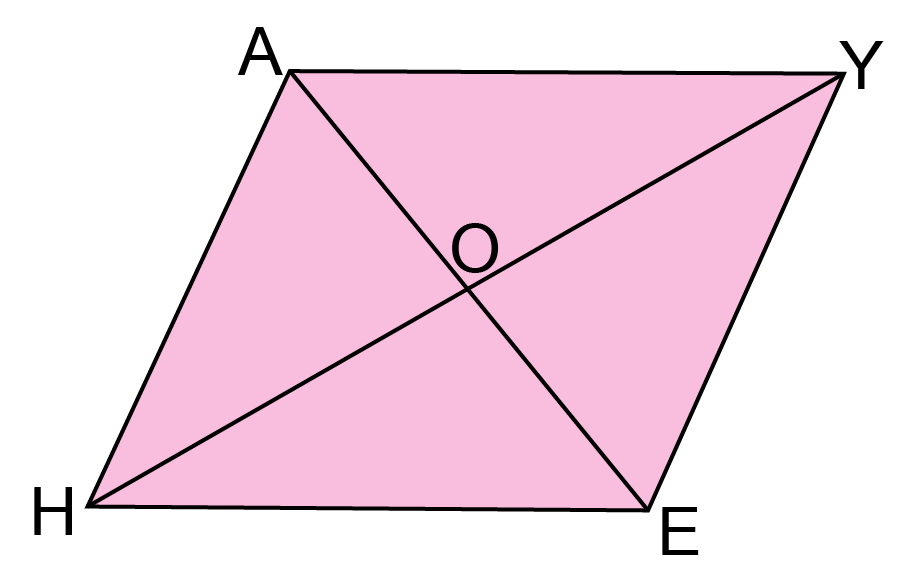
Properties of a Parallelogram: Opposite sides are equal and parallel, opposite angles are equal, and diagonals bisect each other.
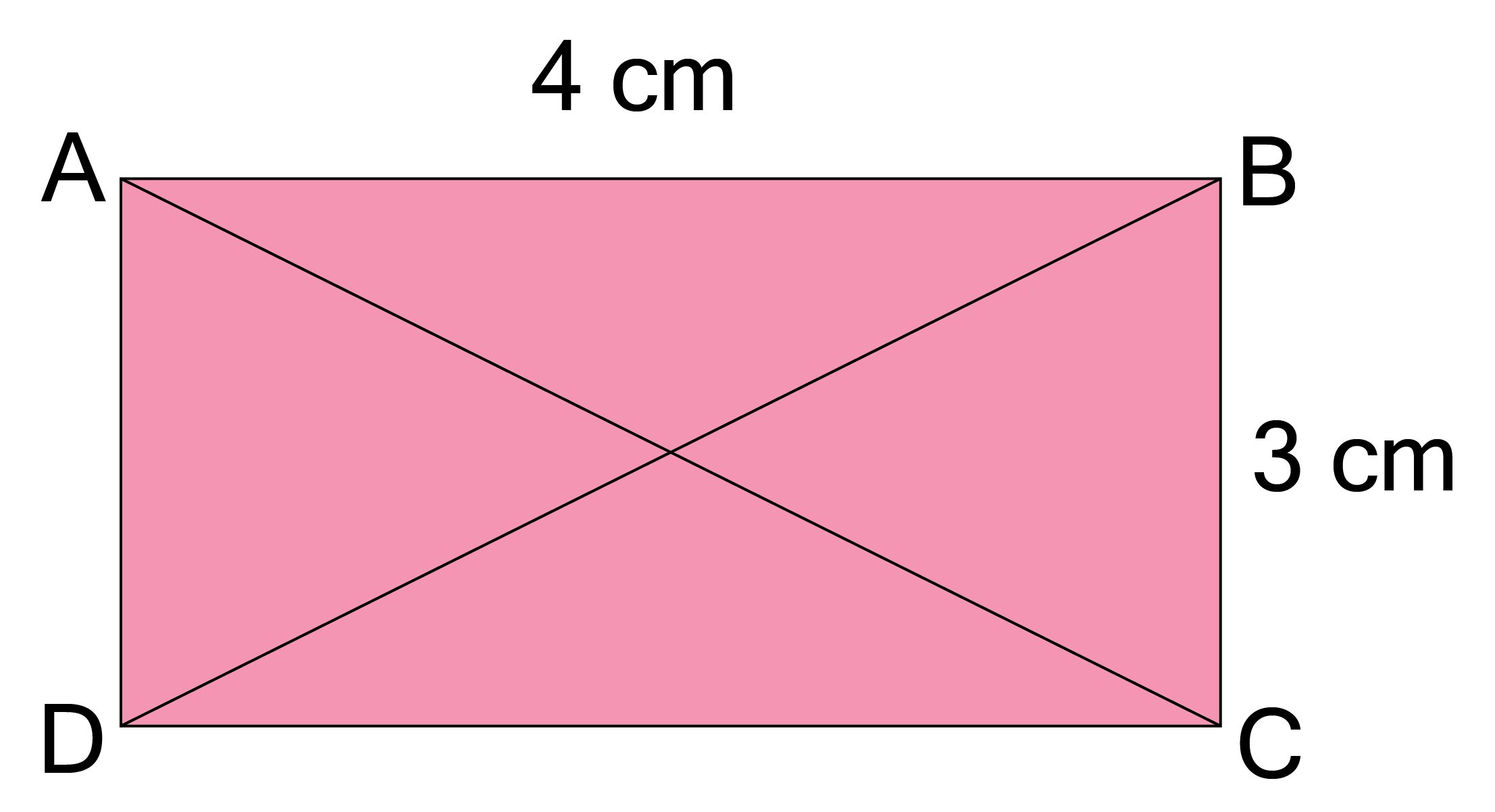
Properties of Special Parallelograms: Know the specific properties of a rhombus (all sides equal, diagonals bisect at 90°), a rectangle (all angles 90°, diagonals are equal), and a square (all properties of a rhombus and rectangle).
2. What types of questions are frequently asked from Chapter 3, Understanding Quadrilaterals, in the CBSE exam?
Based on the 2025-26 exam pattern, you can expect the following types of important questions:
Finding unknown angles or sides of a quadrilateral using its properties.
Questions that require you to identify the type of quadrilateral based on given properties.
Problems involving the properties of diagonals, especially for parallelograms, rhombuses, and rectangles.
Questions based on the sum of exterior angles of a polygon.
3. Why is the angle sum property of a quadrilateral (360°) so important for solving problems?
The angle sum property is a foundational tool because it allows you to create an equation to find an unknown angle if the other three angles are known. In many exam questions, you won't be given all the information directly. You might have to use other properties (like opposite angles of a parallelogram being equal) to find two or three angles first, and then use the angle sum property to find the final missing angle. It is the key that connects all four angles of any quadrilateral.
4. How can I quickly identify different types of parallelograms like a rhombus, rectangle, and square in an exam question?
To quickly identify special parallelograms in an exam, look for these keywords and properties:
If all sides are equal but angles are not 90°, it's a rhombus.
If all angles are 90° but adjacent sides are not equal, it's a rectangle.
If all sides are equal AND all angles are 90°, it's a square.
Pay close attention to the properties of their diagonals. If diagonals are equal, it points towards a rectangle or square. If they bisect at right angles, it indicates a rhombus or square.
5. What is a common mistake to avoid when solving problems about the diagonals of parallelograms?
A very common mistake is assuming that the diagonals of every parallelogram are equal or that they bisect the angles. Remember these crucial distinctions:
All parallelograms have diagonals that bisect each other (cut each other into two equal halves).
Only in a rectangle and a square are the diagonals equal in length.
Only in a rhombus and a square do the diagonals bisect each other at 90 degrees.
Confusing these properties is a frequent cause of losing marks in exams.
6. Which topics from 'Understanding Quadrilaterals' are expected to form 3-mark or 5-mark questions in the 2025-26 exam?
For higher-mark questions (3 or 5 marks), focus on problems that require using multiple properties. For the 2025-26 session, important areas for such questions include:
Finding multiple unknown angles: A problem where you are given a parallelogram with one angle and have to find all other angles of the figure.
Diagonal properties: Questions where you are given lengths of parts of diagonals and have to find unknown variables (e.g., in parallelogram HOPE, OP = 3x+1, OE = 4x-2. Find x).
HOTS questions: Problems that combine the properties of a quadrilateral with concepts from triangles, like proving a figure is a specific type of parallelogram.
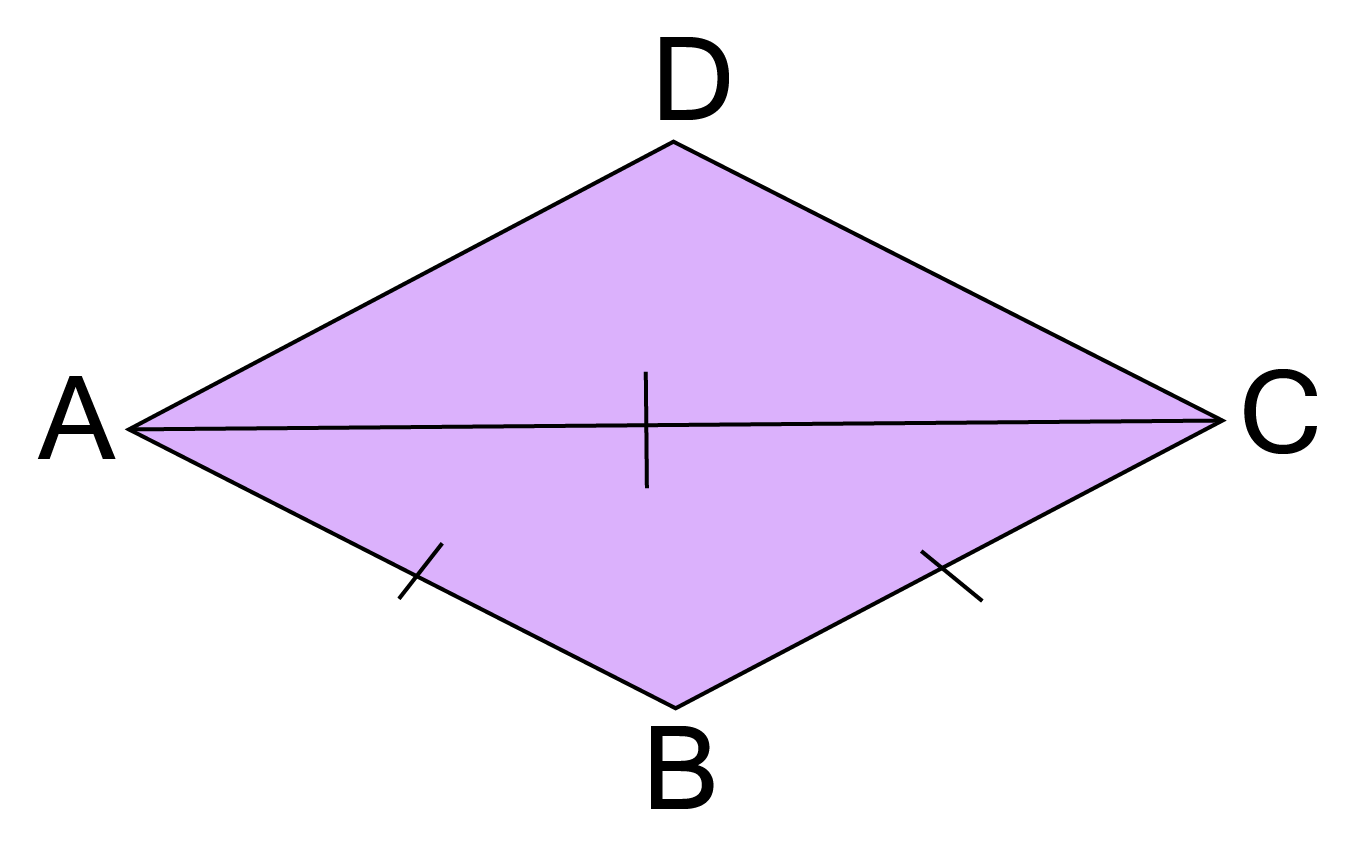
7. How do the properties of a kite differ from a parallelogram, and why is this an important distinction?
This is an important distinction to avoid confusion in 'identify the quadrilateral' type questions. The key differences are:
Sides: A parallelogram has opposite sides equal and parallel. A kite has two pairs of adjacent sides that are equal.
Angles: A parallelogram has opposite angles equal. A kite has only one pair of opposite angles equal.
Diagonals: In a parallelogram, diagonals bisect each other. In a kite, only one diagonal is bisected by the other, and they intersect at a right angle.
Understanding these differences is crucial for applying the correct properties to solve a problem.
8. What is the formula for finding the number of diagonals in a polygon, and how important is it for this chapter?
The formula to find the number of diagonals in a polygon with 'n' sides is n(n-3)/2. This is an important formula for 1-mark or 2-mark objective questions. For example, an important question could be: 'How many diagonals does a hexagon (6 sides) have?'. Using the formula, you would calculate 6(6-3)/2 = 6(3)/2 = 9 diagonals.
9. What kind of Higher Order Thinking Skills (HOTS) questions can be framed from this chapter?
HOTS questions from this chapter go beyond direct application of properties. Expect questions like:
A question asking you to prove that the bisectors of the angles of a parallelogram form a rectangle.
Word problems where you have to model a real-world shape (like a tabletop or a field) as a specific quadrilateral and find its properties or measurements.
A figure where a triangle and a quadrilateral are combined, and you have to use properties of both shapes to find a missing angle or side.
These questions test your deeper conceptual understanding and are important for scoring full marks.
10. What is the best strategy to practise the important questions from Understanding Quadrilaterals before an exam?
An effective strategy is to first create a quick summary chart of all quadrilateral properties. Then, practise the important questions in this order:
Start with 1-mark questions focusing on the angle sum property and identifying figures.
Move to 2 or 3-mark questions involving finding unknown angles and sides in parallelograms.
Finally, tackle the HOTS and 5-mark questions related to the properties of diagonals and proofs.
This tiered approach builds confidence and ensures you master the concepts from simple to complex, as per the CBSE 2025-26 exam pattern.