NCERT Exemplar for Class 8 Maths Solutions Chapter 10 Direct & Inverse Proportions

Solved Examples

1. If x and y are directly proportional and when x = 13,y = 39, which of the following is not a possible pair of corresponding values of x and y ?

(a) 1 and 3 

(b) 17 and 51 

(c) 30 and 10 

(d) 6 and 18

Ans: The correct answer is (c).

As it is said that x and y are directly proportional but in option (c) it contradicts that they are directly proportional as corresponding values of x and y are x > y.

2. A car covers a distance of 40 minutes with an average speed of 60 km per hour. The average speed to cover the same distance in 30 minutes is

(a) 80 km/h 

(b)45 km/h 

(c) 70 km/h 

(d) 45 km/h

Ans: The correct answer is (a).

A car covers a distance of 40 minutes at an average speed is 60km/hr

The same distance can be covered in 1 minute with speed = $\dfrac{60 \times 40}{60}$ = 40km/hr

The same distance can be covered in 30 minutes with speed = $\dfrac{40}{\dfrac{30}{60}} = \dfrac{40}{\dfrac{1}{2}} = 40 \times 2 = 80$km/h

3. Which of the following is in direct proportion?

(a) One side of a cuboid and its volume.

(b) Speed of a vehicle and the distance traveled in a fixed time interval.

(c) Change in weight and height among individuals.

(d) Number of pipes to fill a tank and the time required to fill the same tank.

Ans: The correct answer is (b).

Because, in a fixed time interval, as the speed of a vehicle increases, the distance traveled by it also increases in the same ratio.

In examples 4 to 6, fill in the blanks to make the statements true.

4. Amrita takes 18 hours to travel 720 kilometers. Time taken by her to travel 360 kilometers is _______.

Ans: 9 hours

Distance = Speed $\times$ Time

Speed = $\dfrac{D}{T}$

$\dfrac{D_1}{T_1} = \dfrac{D_2}{T_2}$

$\dfrac{720}{18} = \dfrac{360}{T_2}$

$\dfrac{2}{18} = \dfrac{1}{T_2}$

$2 \times T_2 = 18$

$T_2 = 9$

5. If x and y are inversely proportional then _____ = k where k is a positive constant.

Ans: xy

We say that y varies directly with x or that y is inversely proportional to x if the relationship between variables y and x can be stated in the form y = k x for some constant k. For the relationship, the integer k is referred to as the proportionality constant.

6. Side of a rhombus and its perimeter are in ______ proportion.

Ans: Direct

In examples 7 to 9, state whether the statements are true (T) or false (F):

7. When two quantities x and y are in inverse proportion, then $\dfrac{x}{y}$ is a constant.

Ans: False

When x and y are inverse proportion. I.e., $x \propto \dfrac{1}{y} \Rightarrow xy = k$, where k is some constant

8. If the cost of 10 pencils is Rs 90, then the cost of 19 pencils is Rs 171.

Ans: True

If cost of 10 pencils is Rs 90 then,

Cost of one pencil = $\text{Rs }\dfrac{90}{10} = \text{Rs }9$

Therefore cost of 19 pencils is = Rs 9 $\times$ 19 = Rs 171

9. If 5 people can finish a job in 10 days then one person will finish it in 2 days.

Ans: False

In 10 days, 5 people can complete a task.

One worker may complete the job in = $10\dfrac{5}{1} = 50$days.

It is evident that one person will take longer to complete the same task than the other.

10. In a scout camp, there is food provision for 300 cadets for 42 days. If 50 more persons join the camp, how Will the provision last?

Ans: More the persons, the sooner the provision will be exhausted. So, this is a case of inverse proportion.

Let the required number of days be x.

Hence, 300 × 42 = (300 + 50) × x

300 × 42 = 350 × x

x = 36

11. If two cardboard boxes occupy 500 cubic centimeters of space, then how much space is required to keep 200 such boxes?

Ans: As the number of boxes increases, the space required to keep them also increases.

So, this is a case of direct proportion.

12. Under the condition that the temperature remains constant, the volume of gas is inversely proportional to its pressure. If the volume of gas is 630 cubic centimeters at a pressure of 360 mm of mercury, then what will be the pressure of the gas if its volume is 720 cubic centimeters at the same temperature?

Ans: Given that, at constant temperature pressure and volume

of a gas are inversely proportional. Let the required

pressure be x.

13. Lemons were bought at Rs 60 a dozen and sold at the rate of Rs 40 per 10. Find the gain or loss per cent.

Ans. Let number of men required to finish the job in 10 days be x

No. of days has decreased so the number of men will increase.

Hence we will use inverse variation.

Hence 30 × 17 = x × 10

x= 301710 = 51

51 men will be required.

Extra number of men required = 51 – 30 = 21 men.

Exercises

In questions 1 to 16, there are four options out of which one is correct. Write the correct answer.

1. Both u and v vary directly with each other. When u is 10, v is 15, which of the following is not a possible pair of corresponding values of u and v? 

(a) 2 and 3

(b) 8 and 12

(c) 15 and 20

(d) 25 and 37.5

Ans: u and v vary directly, hence,

$\dfrac{u}{v}= k$ $\left( constant \right)$

Hence, $\dfrac{u}{v} =\dfrac{10}{15} =\dfrac{2}{3}$

Now,

Option (a) $\to  \dfrac{2}{3}$

Option (b) $\to  \dfrac{8}{12} =\dfrac{2}{3}$

Option (c) $\to $ $\dfrac{15}{20} =\dfrac{3}{4}$

Option (d) $\to $ $\dfrac{25}{37.5} =\dfrac{2}{3}$

Therefore, option (c) is not the possible pair of corresponding values of u and v

2. Both x and y vary inversely with each other. When x is 10, y is 6, which of the following is not a possible pair of corresponding values of x and y? (a) 12 and 5

(b) 15 and 4

(c) 25 and 2.4

(d) 45 and 1.3

Ans: Since x and y vary inversely, so

$xy = k$ (constant)

Putting the value of $x$ and $y$, we get,

$10\times 6 = 60$

Now,

Option (a) $\to $ $12 $and$ 5  12\times 5 = 60$

Option (b) $\to  15 $and$ 4  15\times 4 = 60$

Option (c) $\to $ $25 $and$ 2.4  25\times 2.4 = 60$

Option (d) $\to $ $45 $and$ 1.3 = 45\times 1.3 = 58.3$

Therefore, option (d) is not a possible pair of corresponding values of $x$ and $y$

3. Assuming land to be uniformly fertile, the area of land and the yield on it vary

(a) directly with each other.

(b) inversely with each other.

(c) neither directly nor inversely with each other.

(d) sometimes directly and sometimes inversely with each other.

Ans: Since, the land is uniformly fertile, thus more the area of land will give more yield and vice versa. Therefore, area and yield on land vary (a) directly with each other.

4. The number of teeth and the age of a person vary

(a) directly with each other.

(b) inversely with each other.

(c) neither directly nor inversely with each other.

(d) sometimes directly and sometimes inversely with each other.

Ans: Correct option is (d)

The number of teeth and the age of a person vary sometimes directly and sometimes inversely with each other; we cannot predict about the number of teeth with exactly the age of a person. It changes from person-to-person.

5. A truck needs 54 liters of diesel for covering a distance of $297$ km. The diesel required by the truck to cover a distance of $550$ km is

(a) 100 liters

(b) 50 liters

(c) 25.16 liters

(d) 25 liters

Ans: Correct option is (a)

Distance covered by truck using 54 liters diesel = 297 km

Distance covered by truck using 1 liter diesel $=\dfrac{297}{54}$ = 5.5 km

Hence, for 550 km, diesel required $=\dfrac{550}{5.5} $= 100 liters (a)

6. By traveling at a speed of 48 kilometers per hour, a car can finish a certain journey in 10 hours. To cover the same distance in 8 hours, the speed of the car should be

(a) 60 km/h

(b) 80 km/h

(c) 30 km/h

(d) 40 km/h

Ans: Correct option is (a)

Speed of car = 48 km/hr

Time taken = 10 hr

As we know,

Distance = speed $\times $ time $= 48 \times  10=480$ km

Speed required by car to cover 480 km in 8 hours $=\dfrac{480}{8}$ = 60 km/hr (a)

7. In which of the following cases, do the quantities vary directly with each other?

(a)

(b)

(c)

(d)

Ans: Correct option is (a)

The value of x is directly proportional to values of y, such as,

$y = 4x$

If we put the values of $x = 0.5, 2, 8 $and $32,$

we get the values of $y$ as $2, 8, 32$ and $128$ respectively.

i.e If we multiply x with 4, we get the directly required result as the same as shown in corresponding y. In this case, as the value of x increases, the value of y also increases.

8. Which quantities in the previous question vary inversely with each other

(a) x and y

(b) p and q

(c) r and s

(d) u and v

Ans: Correct option is (d)

When the value of u is increasing, the value of v is decreasing. Hence, u and v are inversely proportional.

9. Which of the following vary inversely with each other?

(a) speed and distance covered.

(b) distance covered and taxi fare.

(c) distance traveled and time taken.

(d) speed and time taken.

Ans: Correct option is (d)

By the formula of speed we know,

$Speed =\dfrac{distance}{time}$

As we can see here, when the time decreases, the speed increases. Hence, they are inversely proportional.

10. Both x and y are in direct proportion, then 1 x and 1 y are

(a) in direct proportion.

(b) in inverse proportion.

(c) neither in direct nor in inverse proportion.

(d) sometimes in direct and sometimes in inverse proportion.

Ans: Correct option is (a)

$x\propto y$

Two quantities x and y are said to be in Direct proportion, if an increase in x causes proportional increase in y and vice-versa

$\Rightarrow $     $\dfrac{1}{x}\propto \dfrac{1}{y}$

Thus, $\dfrac{1}{x},\dfrac{1}{y}$ are in direct proportion.

11. Meenakshee cycles to her school at an average speed of 12 km/h and takes 20 minutes to reach her school. If she wants to reach her school in 12 minutes, her average speed should be

(a) $\dfrac{20}{3}$ km/h 

(b) 16 km/h 

(c) 20 km/h 

(d) 15 km/h

Ans: Correct option is (c)

Speed = 12 km/h

Time taken = 20 minutes = $\dfrac{20}{60}$ hr = $\dfrac{1}{3}$ hr

Distance covered = S × T = 12 × $\dfrac{1}{3}$ = 4km

Speed required to cover 4 km in 12 minutes = $\left( \dfrac{4}{12} \right)\times 60$ = 20 km/hr

12. 100 persons had food provision for 24 days. If 20 persons left the place, the provision will last for

(a) 30 days 

(b) $\dfrac{96}{5}$ days

(c) 120 days 

(d) 40 days

Ans: Correct option is (a)

100 persons have food provision for = 24 days

1 person will have food provision for = $24\times 100$ = 2500 days

If 20 persons left the place, then total left = $100-20$ = 80 persons

Hence, 80 persons have food provision for = $\dfrac{2400}{80}$ = 30 days

13. If two quantities x and y vary directly with each other, then

(a) $\dfrac{x}{y}$ remains constant.

(b) x – y remains constant.

(c) x + y remains constant.

(d) x × y remains constant.

Ans: Correct option is (a)

Since, in direct proportion, both x and y increase or decrease together in such a manner that the ratio of their corresponding value remains constant.i.e $\dfrac{x}{y}$ remains constant. 

14. If two quantities p and q vary inversely with each other, then

(a) x y remains constant.

(b) p + q remains constant.

(c) p × q remains constant.

(d) p – q remains constant.

Ans: Correct option is (c)

If two quantities p and q vary inversely with each other, then p x q remains constant. Since, in inverse proportion, an increase in p causes a proportional decrease in q and vice-versa, Hence $p\times q = k$ (constant).

15. If the distance traveled by a rickshaw in one hour is 10 km, then the distance traveled by the same rickshaw with the same speed in one minute is (a) $\dfrac{250}{9}$ m 

(b) $\dfrac{500}{9}$ m 

(c) 1000 m 

(d) $\dfrac{500}{3}$  m

Ans: Correct option is (d)

Distance traveled $= 10$ km

Time taken = 1 hr

In one minute, distance covered $=\dfrac{10}{60}$ km $=\dfrac{10\times 1000}{60}$ m= $\dfrac{500}{3}$ m

16. Both x and y vary directly with each other and when x is 10, y is 14, which of the following is not a possible pair of corresponding values of x and y?

(a) 25 and 35

(b) 35 and 25

(c) 35 and 49

(d) 15 and 21

Ans: Correct option is (b)

$x$ and $y$ are directly proportional.

$i.e., x \propto  y$

If $x = 10$ and $y = 14$, then,

$10 \propto  14$ or $5 \propto  7$

Now, if we compare,

(a) $25 \propto  35 = 5\propto 7$

(b) $35 \propto  25 = 7 \propto  5$

(c) $35 \propto  49 = 5 \propto  7$

(d) $15 \propto  21 = 5 \propto  7$

Therefore, option (b) is not a possible pair of corresponding values of x and y.

17. If $x = 5y$, then x and y vary ______ with each other.

Ans: Given, $x = 5y$

$\Rightarrow \dfrac{x}{y} = \dfrac{5}{1} = k$

Hence  x and y vary directly with each other.

18. If $xy = 10$, then x and y vary ______ with each other.

Ans: Given,  $ xy = 10$

$\Rightarrow  x  = \dfrac{10}{y}  = k$

Hence, x and y vary Inversely with each other.

19. When two quantities x and y are in ______ proportion or vary ______ they are written as $x \propto  y$.

Ans: When two quantities x and y are in direct proportion or vary directly, they are written as $x \propto  y$.

20. When two quantities x and y are in _______ proportion or vary ______ they are written as $x\propto \dfrac{1}{y}$ .

Ans: When two quantities x and y are in indirect proportion or vary indirectly, they are written as $x\propto \dfrac{1}{y}$ .

21. Both $x $and $y$ are said to vary ______ with each other if for some positive number $k$, $xy = k.$

Ans: Both $x $and $y$ are said to vary inversely with each other if for some positive number $k$, $xy = k.$

22. $x$ and $y$ are said to vary directly with each other if for some positive number $k,$ ______ $=k.$

Ans: $x$ and $y$ are said to vary directly with each other if for some positive number $k,$ $ \dfrac{x}{y}$ = $k.$

23. Two quantities are said to vary ______ with each other if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant.

Ans: Two quantities are said to vary directly with each other if they increase (decrease) together in such a manner that the ratio of their corresponding values remains constant.

24. Two quantities are said to vary __________ with each other if an increase in one causes a decrease in the other in such a manner that the product of their corresponding values remains constant.

Ans: Two quantities are said to vary inversely with each other if an increase in one causes a decrease in the other in such a manner that the product of their corresponding values remains constant.

25. If 12 pumps can empty a reservoir in 20 hours, then time required by 45 such pumps to empty the same reservoir is ______ hours.

Ans: Time taken by 12 pumps to empty a reservoir = 20 hr

Time taken by 1 pump to empty the reservoir $= 20 \times  12 = 240$ hr

Hence, time taken by 45 pumps to empty the reservoir

$=\dfrac{240}{45}=\dfrac{240\times 60}{45}=\dfrac{14400}{45} =$ 320 min$= 5\times 60+20$ min= $5$ hour $20$ min

26. If x varies directly as y, then

Ans: If x varies inversely as y, then,

$     x\times y = k$

$\Rightarrow $ If$ x = 60$ and $y = 10$

Then,

$ x\times y = 60\times 10 = 600 = k$

Hence, $x\times 2 = 600$

$\Rightarrow $ $x      =\dfrac{600}{2}= 300$

27. If x varies directly as y, then

Ans: If $x$ and $y $varies directly, then,

$\dfrac{x}{y} = k$

If $x=12$ and$ y = 48$, then

$\Rightarrow $  $k =\dfrac{12}{48}=\dfrac{1}{4}$

Now, if $x=6$, and $k =\dfrac{1}{4},$ then y will be,

$       \dfrac{6}{y} =\dfrac{1}{4}$

$\Rightarrow $  $y = 6\times 4=24$

28. When the speed remains constant, the distance traveled is ______ proportional to the time.

Ans: When the speed remains constant, the distance traveled is directly proportional to the time.

29. On increasing a, b increases in such a manner that a/b remains _______ and positive, then a and b are said to vary directly with each other

Ans: On increasing a, b increases in such a manner that a/b remains constant and positive, then a and b are said to vary directly with each other.

30. If on increasing a, b decreases in such a manner that ab remains ________ and positive, then a and b are said to vary inversely with each other.

Ans: If on increasing a, b decreases in such a manner that ab remains constant and positive, then a and b are said to vary inversely with each other.

31. If two quantities x and y vary directly with each other, then ________ of their corresponding values remains constant.

Ans: If two quantities x and y vary directly with each other, then ratio of their corresponding values remains constant.

32. If two quantities p and q vary inversely with each other then, _________ of their corresponding values remains constant.

Ans: If two quantities p and q vary inversely with each other then, product of their corresponding values remains constant.

33. The perimeter of a circle and its diameter vary ________ with each other.

Ans: The perimeter of a circle and its diameter vary directly with each other.

34. A car is traveling 48 km in one hour. The distance traveled by the car in 12 minutes is _________.

Ans: Distance traveled by car in one hour $= 48$ km

Distance traveled in one minute $=\dfrac{48}{60}$ km

Distance traveled in 12 minutes $= \left( \dfrac{48}{60} \right)\times 12 =\dfrac{48}{5} = 9.6$ km

35. An auto rickshaw takes 3 hours to cover a distance of 36 km. If its speed is increased by 4 km/h, the time taken by it to cover the same distance is __________.

Ans: Distance covered by auto rickshaw in 3 hours $= 36$ km

Speed $=\dfrac{36}{3} =$ 12 km/hr

If we increase the speed by 4km/hr, then the total speed becomes $= 12+4 = 16 $km/hr

Now, the time taken by auto rickshaw will be = $\dfrac{36}{16} =\dfrac{36\times 60}{16}$ = 135 min

$= 120 + 15$= 2-hour 15min

36. If the thickness of a pile of 12 cardboard sheets is 45 mm, then the thickness of a pile of 240 sheets is _______ cm.

Ans: Thickness of pile of 12 cardboard sheets = 45 mm

Thickness of 1 cardboard sheet = $\dfrac{45}{12}$ mm

Hence, thickness of a pile of 240 sheets $= \left( \dfrac{45}{12} \right)\times 240$= $900$ mm$=\dfrac{900}{10}cm = 90$ cm

37. If x varies inversely as y and x = 4 when y = 6, then when x = 3 the value of y is _______.

Ans: If $x$ varies inversely as $y$, then

$ x\times y= k$

$\Rightarrow   4\times 6= k$

$\Rightarrow $ $k=24$

Now, if $x = 3$, then $y$ is:

$y =\dfrac{k}{x} =\dfrac{24}{3} = 8$

38. In direct proportion, $\dfrac{a_1}{b_1}$  _______ $\dfrac{a_2}{b_2}$

Ans: $\dfrac{a_1}{b_1} = \dfrac{a_2}{b_2} = k$

$\Rightarrow \dfrac{a_1}{a_1} = k = $ constant

39. In case of inverse proportion, $\dfrac{a_1}{_} = \dfrac{b_2}{_}$ 

Ans: In inverse proportion

$\dfrac{a_1}{b_1} = \dfrac{a_2}{b_2} = k$

$\Rightarrow \dfrac{a_1}{a_2} = \dfrac{b_2}{b_1} = $ constant

40. If the area occupied by 15 postal stamps is 60 cm2, then the area occupied by 120 such postal stamps will be _______.

Ans: Area occupied by 15 postal stamps = 60cm2

Area occupied by 1 postal stamp $=\dfrac{60}{15}$ = 4 cm2

Area occupied by 120 such postal stamps $= 4\times 120 =480$ cm2

41. If 45 persons can complete a work in 20 days, then the time taken by 75 persons will be ______ hours.

Ans: 45 persons complete a work in 20 days

1 person can complete work in = $45 \times  20 = 900$ days

Time taken by 75 persons$ =\dfrac{900}{75}$ = 12 days = $12\times 24 = 288$ hr

42. Devangi travels 50 m distance in 75 steps, then the distance traveled in 375 steps is _______ km.

Ans: Distance traveled in 75 steps $= 50$ m

Distance covered in 1 step = $\dfrac{50}{75} $m

Distance covered in 375 steps $= \left( \dfrac{50}{75} \right)\times 375=$ $\dfrac{18750}{75}$= 250 m= $\dfrac{250}{1000}$  km= 0.25km

In questions from 43 to 59, state whether the statements are true (T) or false (F).

43. Two quantities $x$ and $y$ are said to vary directly with each other if for some rational number k, $xy = k.$

Ans: False, Two quantities x and y are said to vary directly with each other, if

$x\propto y$

$\Rightarrow  x=ky$

44. When the speed is kept fixed, time and distance vary inversely with each other.

Ans: False, When the speed is kept fixed, time and distance vary directly with each other.

$\text{Speed}=\dfrac{\text{distance}}{\text{time}}$

Since, speed is fixed so,

$Const\propto \dfrac{d}{t} \Rightarrow t\propto d$

45. When the distance is kept fixed, speed and time vary directly with each other.

Ans: False, When the distance is kept fixed, speed and time vary indirectly/inversely with each other. Since, if we increase speed, then time taken will be less and vice-versa.

$\text{Speed}=\dfrac{\text{distance}}{\text{time}}$

Since, distance is fixed so,

$s\propto \dfrac{1}{t}$

46. Length of a side of a square and its area vary directly with each other.

Ans: False, Length of a side of a square and its area does not vary directly with  each other, e.g.

Let a be the length of each side of a square.$  Area={{a}^{2}}$

So, if we increase the length of the side of a square, then their area increases but not directly.

47. Length of a side of an equilateral triangle and its perimeter vary inversely with each other.

Ans: False, Length of a side of an equilateral triangle and its perimeter vary directly with each other, e.g. Let a be the side of an equilateral triangle

$\text{Perimeter}=3\times \text{Side} \Rightarrow \text{Perimeter} \propto \text{Side}$

So, if we increase the length of the side of the equilateral triangle, then their     perimeter will also increase.

48. If d varies directly as t2, then we can write dt2 = k, where k is some constant.

Ans: False, If d varies inversely as $t^2$, then we can write $dt^2 = k$, where k is some constant.

Since, two quantities x and y are said to be in Inverse proportion, if an increase in x causes a proportional decrease in y and vice-versa, in such a manner that the product of their corresponding values remains constant.

49. If a tree 24 m high casts a shadow of 15 m, then the height of a pole that casts a shadow of 6 m under similar conditions is 9.6 m.

Ans: True

Height of tree $= 24$ m

Length of shadow of tree $= 15$ m

Let height of pole $= x$

Length of shadow of pole $= 6$ m

Now,

$\dfrac{24}{15} =\dfrac{x}{6}$

$\Rightarrow  x =\dfrac{24\times 6}{15}$

$\Rightarrow x =9.6$ m

50. If $x$ and $y$ are in direct proportion, then (x-1) and (y-1) are also in direct proportion.

Ans: False

$x$ and $y$ are in direct proportion, then,

$\dfrac{x}{y} = k$

if $x = 3$ and $y = 5$, then

$\Rightarrow k =\dfrac{3}{5}$

Now, $x-1 = 2$ and $y-1=4$

$\Rightarrow $  $\dfrac{x-1}{y-1}=\dfrac{2}{4} =\dfrac{1}{2}$

51. If x and y are in inverse proportion, then (x +1) and (y +1) are also in inverse    proportion

Ans: False, If x and y are in inverse proportion,

then xy = k (constant) e.g. Let x= 2 and y = 3

∴ xy = 2 x 3= 6.

Now, x + 1=2 + 1 = 3 and y+ 1 = 3 + 1 = 4

Then, (x + 1)(y+1) = 3 x 4 = 12 [not in inverse proportion]

Hence, (x+ 1)and (y + 1) cannot be in inverse proportion.

52. If p and q are in inverse variation then (p + 2) and (q – 2) are also in inverse    proportion.

Ans: False, If p and q are in inverse proportion, then xy = k (constant)

e.g. Let p = 3 and q = 4

Then, pq = 3×4 = 12

Now, p+ 2 = 3+ 2 = 5 and q-2 = 4-2 =2

(p + 2) (q – 2) = 5 x 2 = 10 [not in inverse proportion]

Hence, (p+2) and (q -2) cannot be in inverse proportion.

53. If one angle of a triangle is kept fixed, then the measure of the remaining two angles vary inversely with each other.

Ans: False,If one angle of a triangle is kept fixed, then the measure of the remaining two angles cannot vary inversely with each other.

Let’s assume a triangle-

$\angle A$+ $\angle B$+ $\angle C$ = 180 (sum of all angles)

if $\angle $A=50 then $\angle $B+$\angle $C=180-50=130

Angle sum properties of a triangle don’t depend on any proportion.

54. When two quantities are related in such a manner that, if one increases, the other also increases, then they always vary directly.

Ans: True, When two quantities are related in such a manner that if one increases the other also increases, then they always vary directly.

Above statement is correct for direct proportion. It is a basic property of direct proportion.

55. When two quantities are related in such a manner that if one increases and the other decreases, then they always vary inversely.

Ans: True, When two quantities are related in such a manner that if one increases and the other decreases, then they always vary inversely. Above statement is correct for inverse proportion. It is a basic property of inverse proportion.

56. If $x$ varies inversely as $y$ and when $x = 6, y = 8$, then for $x = 8, $the value of $y$ is $10$.

Ans: False

If x varies inversely as y i.e. $xy = k$ (constant)

If $x = 6$ and $y =8$ ,

$xy = 6\times 8=48$.

But if $x=8$ and $y= 10$,

$xy = 8\times 10=80$.

Here $48\ne 80,$

Hence, the value of y is not 10.

57. The number of workers and the time to complete a job is a case of direct proportion.

Ans: False.
The number of workers and the time to complete a job is a case of indirect proportion, e.g. If 60 workers can complete a work in 10 days. Then, 120 workers can complete the same work in 5 days.

58. For fixed time period and rate of interest, the simple interest is directly proportional to the principal.

Ans: True. For fixed time period (T) and rate of interest (R), the simple interest is directly proportional to the principal.

We know that,

$SI=\dfrac{P\times R\times T}{100}$

$\Rightarrow   \dfrac{SI}{P}=R\times \dfrac{T}{100}=Constant \left(  As R \And  T are constants  \right)$

Therefore, Simple interest is directly proportional to the principal.

59. The area of cultivated land and the crop harvested is a case of direct proportion.
Ans: True
The area of cultivated land and the crop harvested is a case of direct proportion.
Since, the quantity of crop harvested is dependent upon the area of cultivated land.

In questions 60 to 62, which of the following vary directly and which vary inversely with each other, and which are neither of the two?

60. (i)The time taken by a train to cover a fixed distance and the speed of the train.
Ans: The time taken by a train to cover a fixed distance and the speed of the train are inversely proportional.

e.g. Let a train cover 200 km in 1 h with speed 200 km/h.

Then, the same train covers 200 km in 30 min with speed 400 km/h.

(ii) The distance traveled by CNG bus and the amount of CNG used.

Ans: The distance traveled by CNG bus and the amount of CNG used are directly proportional.
e.g. Let a CNG bus travel 10 km in 1 kg of CNG.

Then, the same CNG bus traveled 20 km in $2 \times 1 = 2$ kg of CNG.

(iii) The number of people working and the time to complete a given work.

Ans: The number of people working and the time to complete a given work are inversely proportional to each other.

e.g. Let 20 workers complete a work in 2day.

Then, 10 workers can complete the same work in 4 days.

(iv) Income tax and the income.

Ans: Income tax and the income are directly proportional to each other, e.g. Let Mr. X have$4.5$ lakh annual income.

Then, he pays $10%$ income tax on his income.

But if Mr. X has $5.5$ lakh annual income, then he has to pay $30%$ income tax on his salary/income.

(v) Distance traveled by an auto-rickshaw and time taken.

Ans: Distance traveled by an auto rickshaw and time taken are directly proportional to each other.e.g. Let an auto rickshaw takes 2 h to travel 10 km. Then, it will take 4 h to travel 20 km.

61. (i) Number of students in a hostel and consumption of food.

Ans: Number of students in a hostel and consumption of food are directly proportional to each other. For example: let 200 students in a hostel consume 100 kg of rice in a month. Then, 400 students in a hostel can consume 200 kg of rice in a month.

(ii) Area of the walls of a room and the cost of whitewashing the walls.

Ans: Area of the walls of a room and the cost of white washing the balls are directly proportional to each other.

For example: let ₹10000 required for white washing a room with $\left( 12\times 8 \right)m$ size.

Then, ₹20000 required for white washing a room with $\left( 12\times 16 \right)m$ size.

(iii) The number of people working and the quantity of work.

Ans: The number of people working, and the quantity of work are directly proportional to each other.

For example: let 200 workers complete 20% of our work.

Then, 400 workers can complete 40% of the same work.

(iv) Simple interest on a given sum and the rate of interest.

Ans: Simple interest on a given some under rate of interest are directly proportional to each other.

For example: Let P = ₹1000, R = 10% and T = 1yr

$SI=\dfrac{P\times R\times T}{100}=\dfrac{1000\times 10\times 1}{100}=$ ₹ 100

But if P = ₹1000, R = 20% and T = 1yr

$SI=\dfrac{P\times R\times T}{100}=\dfrac{1000\times 20\times 1}{100}=$ ₹ 200

(v) Compound interest on a given sum and the sum invested.

Ans: Compound interest on some under some investors are neither dependent directly or inversely.

62. (i) The quantity of rice and its cost.

Ans: The quantity of rice and its cost are directly proportional to each other, e.g. 

Let 1 kg of rice price = Rs 40

Then, 2 kg of rice price $= Rs 2\times 40 = Rs 80$

(ii) The height of a tree and the number of years.

Ans: The height of a tree and the number of years is neither directly nor inversely proportional to each other.

(iii) Increase in cost and number of shirts that can be purchased, if the budget remains the same.

Ans: Increase in cost and number of shirts that can be purchased, if the budget remains the same are inversely proportional to each other.

E.g.: Let 2 shirts price = Rs 800

After increasing the price of each shirt,1 shirt price became Rs 800 where budget = Rs 800.

(iv) Area of land and its cost.

Ans: Area of land and its cost are directly proportional to each other.

E.g., Let $200{{m}^{2}}$ land cost = Rs. 1000

Then, $400{{m}^{2}}$ land cost = Rs. 2000

(v) Sales tax and the amount of the bill.

Ans: Sales tax and the amount of the bill are directly proportional to each other.

e.g. Let bill amount = Rs. 1000

Sales tax = 10%

Then, sales tax $=\dfrac{10}{100}\times 1000=Rs. 100$

But if, bill amount = 2000

Sales tax = 10%

Then, sales tax = $\dfrac{10}{100}\times 2000=10\times 20=Rs. 200$

63. If x varies inversely as y and x = 20 when y = 600, find y when x = 400.

Ans: If $x$ varies inversely with $y$,

$xy = k$ (constant) .... (i)

If$ x = 20$ and $y = 600 $

$xy = 20\times 600      $

$ =12000  $

$k = 12000  $

When $x = 400$ then from equation-(i),

$ \Rightarrow $   $y\times 400=k $

$\Rightarrow $   $y\times 400=12000 $

$\Rightarrow $  $y = 30  $

64. The variable x varies directly as y and x = 80 when y is 160. What is y when x is 64?

Ans: If x varies directly as y

$ \dfrac{x}{y}=k$

If $x = 80 $and $y = 160$

$\Rightarrow $   $\dfrac{x}{y}=\dfrac{80}{160}=\dfrac{1}{2}$

When $x = 64$,

$ \dfrac{64}{y}=\dfrac{1}{2}$

$\Rightarrow   y=128$

65. l varies directly as m and l is equal to 5, when m = $\dfrac{2}{3}$. Find l when m = $\dfrac{16}{3}.$

Ans: If l varies directly as m,

$\dfrac{l}{m}=\dfrac{5}{\dfrac{2}{3}}\ldots \left( i \right)$

$\dfrac{l}{m} =5\times \dfrac{3}{2}=\dfrac{15}{2}$

$\Rightarrow k=\dfrac{15}{2}$

When $m=\dfrac{16}{3}, $then from (i),

$\dfrac{l}{\dfrac{16}{3}}=\dfrac{15}{2}$

$\Rightarrow $   $l=\dfrac{15}{2}\times \dfrac{16}{3}=40$

66. If $x$ varies inversely as $y$ and $y =60$ when $x = 1.5$. Find $x$ when $y = 4.5$.
Ans: If $x$ varies inversely as y

$xy=k$ (constant) …(i)

If $x=1.5$ and $y=60$

$\therefore xy=1.5\times 60=90$

$\Rightarrow $ $k=90$

When $y=4.5,$then from Eq. (i)

$4.5\times y=k$

$\Rightarrow 4.5\times y=90$

$\Rightarrow  y=\dfrac{90}{4.5}=20$

67. In a camp, there is enough flour for 300 persons for 42 days. How long will  the flour last, if 20 more persons join the camp?

Ans: Since, for 300 people, flour is enough for 42 days.

Therefore, for 1 person flour enough$=300\times 42=12600$ days

Now, 20 more people have joined the camp.

So, total persons$=300+20=320$

Therefore, for 320 persons flour enough $=\dfrac{12600}{320}=\dfrac{3}{8}$ days

68. A contractor undertook a contract to complete a part of a stadium in 9 months with a team of 560 persons. Later on, it was required to complete the job in 5 months. How many extra persons should he employ to complete the work?

Ans: 560 people complete it partially in 9 months

$\therefore $1 person completes it in 9×560= 5040

$\therefore $ In 5 months the work can be completed =$\dfrac{5040}{5}$=1008 persons

Now, the number of extra persons should he employ to complete the work in 5 months

=1008-560=448 persons

69. Sobi types 108 words in 6 minutes. How many words would she type in half an hour?

Ans: 1 hour = 60 minutes $\Rightarrow $Half hour = 30 minutes

In 6 minutes Sobi can type = 108 words

In 1 minute she can type = $\dfrac{108}{6}$

In 30 minutes she can type = $\dfrac{108}{6}\times $ 30 = 540 words

70. A car covers a distance in 40 minutes with an average speed of 60 km/h. What should be the average speed to cover the same distance in 25 minutes?

Ans: car covers a distance in 40 min with an average speed =60km/h = $\dfrac{60 \times 1000}{60}$m/min

In 1 min, the same distance can be cover with speed =$\dfrac{60 \times 1000\times 40 }{60}$= 40000 m/min

In 25 min, the same distance can be cover with speed = $\dfrac{40000 }{25}$= 1600 m/min

= $\dfrac{1600 }{1000}$ $\times  60$ = 16 $\times  6$ = 96  km/h

71. It is given that l varies directly as m.

(i) Write an equation which relates l and m.

Ans: Since l varies directly as m

Equation related to l and m is $\dfrac{l}{m}$ = k(constant)

(ii) Find the constant of proportion (k), when l is 6 then m is 18.

Ans: If l = 6 and m = 18 then k= $\dfrac{6}{18}$ = $\dfrac{1}{3}$

(iii) Find l, when m is 33.

Ans: If m = 33, then

$\dfrac{l}{m}$ =$\dfrac{1}{3}$

$\Rightarrow $ $\dfrac{l}{33}$ =$\dfrac{1}{3}$

$\Rightarrow $ l = 33 ($\dfrac{1}{3}$) $\Rightarrow $ l = 11

(iv) Find m when l is 8.

Ans: If l = 8, then

$\dfrac{l}{m}$ =$\dfrac{1}{3}$

$\Rightarrow $ $\dfrac{8}{m}$ =$\dfrac{1}{3}$

$\Rightarrow $ m = 8 (3) $\Rightarrow $ l = 24

72. If a deposit of Rs 2,000 earns an interest of Rs 500 in 3 years, how much interest would a deposit of Rs 36,000 earn in 3 years with the same rate of simple interest?

Ans: If deposit of Rs 2000 earns in 3yr with an interest = Rs500

Then, a deposit of Rs1000 earns in 3yr with an interest =$\dfrac{500}{2}$ = 250

Similarly, deposit of Rs 3600 i.e.

Rs. 36 × 1000 earns in 3yr with an interest = 250 × 36 = Rs 9000

73. The mass of an aluminum rod varies directly with its length. If a 16 cm long rod has a mass of 192 g, find the length of the rod whose mass is 105 g.

Ans: In direct proportion,$\dfrac{m}{l}$ = k $\Rightarrow $ $\dfrac{192}{16}$ = 12 =k

If mass of the rod=105g

$\dfrac{m}{l}$ = k    $\Rightarrow $ $\dfrac{105}{l}$ = 12 $\Rightarrow $ $\dfrac{105}{12}$ = l $\Rightarrow $ l =8.75 cm

74. Find the values of x and y if a and b are in inverse proportion:

a. 12 × 8

b. 305 y

Ans: Given,

In part a, the value of x

x=12×6=72

In part b the value of y

y = 5×9=45

75. If Naresh walks 250 steps to cover a distance of 200 meters, find the distance traveled in 350 steps.

Ans: 250 steps covers a distance =200 meter

1 step covers = $\dfrac{200}{250}$

350 steps cover = $\dfrac{200}{250}$ $\times $ 350 =  $\dfrac{4}{5}$ $\times $ 350 = 4 $\times $ 70 = 280

76. If Naresh walks 250 steps to cover a distance of 200 meters, find the distance traveled in 350 steps.

Ans: 225 km travels in =25 ltr

1 km travel = $\dfrac{25}{225}$

540 km will require = $\dfrac{25}{225}$ $\times $ 540 =  $\dfrac{20}{60}\dfrac{1}{9}$ $\times $ 540 = 60

77. From the following table, determine if x and y are in direct proportion or not.

(i)

Ans: $\dfrac{x}{y}$ =  $\dfrac{3}{12}$, $\dfrac{6}{24}$,$\dfrac{15}{45}$ ,$\dfrac{20}{60}$ , $\dfrac{30}{120}$ $\Rightarrow $ $\dfrac{1}{4}$,$\dfrac{1}{4}$,$\dfrac{1}{3}$,$\dfrac{1}{3}$,$\dfrac{1}{4}$

Therefore, (i) is not in direct proportion

(ii)

Ans: $\dfrac{x}{y}$ =  $\dfrac{4}{24}$, $\dfrac{7}{42}$,$\dfrac{15}{45}$ ,$\dfrac{10}{60}$ , $\dfrac{16}{96}$ $\Rightarrow $ $\dfrac{1}{6}$,$\dfrac{1}{6}$,$\dfrac{1}{6}$,$\dfrac{1}{6}$,$\dfrac{1}{6}$

Therefore (ii) is in direct proportion

(iii)

Ans: $\dfrac{x}{y}$ =  $\dfrac{1}{1.5}$, $\dfrac{4}{6}$,$\dfrac{9}{13.5}$ ,$\dfrac{20}{30}$ $\Rightarrow $ $\dfrac{2}{3}$,$\dfrac{2}{3}$,$\dfrac{2}{3}$,$\dfrac{2}{3}$

Therefore (iii) is in direct proportion

78. If a and b vary inversely to each other, then find the values of p, q, r; x, y, z and l, m, n.

(i)

Ans: a $\times $ b = 6  $\times $ 18 = 8 $\times $ p = q  $\times $ 39 = 25  $\times $ r = k

$\Rightarrow $ 108 = 8 $\times $ p = q  $\times $ 39 = 25  $\times $ r = k

Hence , p= $\dfrac{108}{8}$  , q = $\dfrac{108}{39}$ , r= $\dfrac{108}{25}$

$\Rightarrow $ p= $\dfrac{27}{2}$  , q = $\dfrac{36}{13}$ , r= $\dfrac{108}{25}$

(ii)

Ans: a $\times $ b = 2$ \times $ x = y $\times $ 12.5 = 6 $\times $ 15 = 10  $\times $ z = k

$\Rightarrow $ 90 = 2 $\times $ x = y  $\times $ 12.5 = 10  $\times $ z

Hence , x= $\dfrac{90}{2}$  , y = $\dfrac{90}{12.5}$ , z= $\dfrac{90}{10}$

$\Rightarrow $ x=45  , y =7.2 , z=9

(iii)

Ans: a $\times $ b = l $\times  $5 = 9 $\times $ m = n $\times $ 25 =  6 $\times $ 10 = k

$\Rightarrow $ 60 = 5l = 9m = 25n

Hence , x= $\dfrac{60}{5}$  , y = $\dfrac{60}{9}$ , z= $\dfrac{60}{25}$

$\Rightarrow $ x=12  , y =$\dfrac{20}{3}$ , z=$\dfrac{12}{5}$=2.4

79. If 25 meters of cloth costs Rs 337.50, then

(i) What will be the cost of 40 meters of the same type of cloth?

Ans: 25 meter cloth costs = Rs. 337.50

1 meter cloth cost = $\dfrac{337.5}{25} $= Rs.13.5

40 meter clothe cost = 13.5×40 = Rs. 540

(ii) What will be the length of the cloth bought for Rs 810?

Ans:  25 meter cloth costs = Rs. 337.50

1 meter cloth cost = $\dfrac{337.5}{25} $= Rs.13.5

In Rs 810 clothe can be purchased = $\dfrac{1}{13.5}$  $\times $ 810=60meter

80. A swimming pool can be filled in 4 hours by 8 pumps of the same type. How many such pumps are required if the pool is to be filled in 2$\dfrac{2}{3}$ hours?

Ans: To fill the tank in 1 hour total pumps required = 4×8=32

Total time = 2$\dfrac{2}{3}$ hours = $\dfrac{8}{3}$ hours

Total mumps required =  32 $\div  \dfrac{8}{3}$ = $\dfrac{32 \times 3}{8}$ = 12 pumps

81. The cost of 27 kg of iron is Rs 1,080, what will be the cost of 120 kg of iron of the same quality?

Ans: 27 kg iron costs = Rs 1080

1 kg iron cost=$\dfrac{1080}{27}$  =Rs. 40

120 kg iron will cost = 120 × 40=Rs. 4800

82. At a particular time, the length of the shadow of Qutub Minar whose height is 72 m is 80 m. What will be the height of an electric pole, the length of whose shadow at the same time is 1000 cm?

Ans: Length of Qutub Minar = 72m

At a particular time its shadow = 80m

Shadow of the electric pole has a length of = 1000cm=10m

Length of electric pole =  $\dfrac{72}{80}$ $\times $ 100 =   9m

83. In a hostel of 50 girls, there are food provisions for 40 days. If 30 more girls join the hostel, how long will these provisions last?

Ans:50 girls can have the food = 40 Days

1 girl can have the food = 50×40=2000 Days

Total Girls = 50+30 =80

80 girls can have = $\dfrac{2000}{80}$ =25 Days

84. The Campus and Welfare Committee of the school is planning to develop a blue shade for painting the entire school building. For this purpose various shades are tried by mixing containers of blue paint and white paint. In each of the following mixtures, decide which a lighter shade of blue is and also find the lightest blue shade among all of them.

If one container has one liter paint and the building requires 105 liters for painting, how many containers of each type is required to paint the building in the darkest blue shade?

Ans: (i) In mixture A

Ratio of blue and white = $\dfrac{3}{4}$

In mixture B

Ratio of blue and white=  $\dfrac{3}{3}$=1

Clearly mixture A will have a lighter shade

(ii) In mixture C

Ratio of blue and white = $\dfrac{3}{3}$=1

In mixture D Ratio

on blue and white = $\dfrac{2}{5}$=0.4

Clearly mixture D will have a lighter shade.

(iii) In mixture E

Ratio of blue and white=$\dfrac{6}{1}$=6

In mixture F

Ratio of blue and white= $\dfrac{4}{2}$=2

Clearly mixture F will have a lighter shade.

(iv) In mixture G

Ratio of blue and white=$\dfrac{3}{3}$=1

In mixture H Ratio of blue and white=$\dfrac{4}{3}$=1.33

Clearly mixture G will have a lighter shade.

85. Posing a question:

Work with a partner to write at least five ratio statements about this quilt, which has white, blue, and purple squares?

How many squares of each color will be there in 12 such quilts?

Ans: Purple = 12, Blue = 20 and white = 16

Total squares = 12+20+16=48

Statement I Purple: Totala = 12:48=5:12

Statement II Blue: Total = 20:48=1:3

Statement III White: Total = 16:48=1:3

Statement IV Purple: Blue= 12:20=3:5

Statement V Purple: White= 12:16=3:4

86. A packet of sweets was distributed among 10 children and each of them received 4 sweets. If it is distributed among 8 children, how many sweets will each child get?

Ans: 10 children received = 4 sweets

1 child receives = 10×4=40

8 children receive =$\dfrac{40}{5}$ = 8 sweets

87. 44 cows can graze a field in 9 days. How many less/more cows will graze the same field in 12 days?

Ans: 9 days take to graze the field by = 44 cows

1 day will take more cows to graze = 44×9

12 days will take fewer cows to graze = $\dfrac{44 \times  9}{12}$ = 33 cows

Decreased number of cows = 44-33=11

88. 30 persons can reap a field in 17 days. How many more people should be engaged to reap the same field in 10 days?

Ans: 17 days need to reap the field by =30 persons

1 day need to reap the field by more man= 30×17=510

10 days need to reap filed by less men= $\dfrac{510}{10}$ = 51 men

89. Shabnam takes 20 minutes to reach her school if she goes at a speed of 6 km/h. If she wants to reach school in 24 minutes, what should be her speed?

Ans: 20 minutes time Shabnam takes to reach with the speed =6km/hr

1 minute time will take a speed = 6×20=120km/hr

24 minutes time will take with a speed = $\dfrac{120}{24}$ = 5km / hr

90. Ravi starts for his school at 8:20 a.m. on his bicycle. If he travels at a speed of 10km/h, then he reaches his school late by 8 minutes but on traveling at 16 km/h he reaches the school 10 minutes early. At what time does school start?

Ans: Let the total distance = x km

Time taken = t min

With speed of bicycle 10km/hr , then he reaches by 8 min

$\dfrac{x}{10}$ = t+ $\dfrac{8}{60}$ $\Rightarrow $ $\dfrac{x}{10}$ = t+ $\dfrac{2}{15}$…(1)

With speed 16km/hr then reaches his school 10 min early

$\dfrac{x}{16}$ = t- $\dfrac{10}{60}$ $\Rightarrow $ $\dfrac{x}{16}$ = t-$\dfrac{1}{6}$ …(2)

On subtracting (2) from (1)

$\dfrac{x}{10}$ - $\dfrac{x}{16}$ = $\dfrac{2}{15}$ + $\dfrac{1}{6}$

$\Rightarrow $  $\dfrac{8x-5x}{80}$ = $\dfrac{4+5}{30}$

$\Rightarrow $  $\dfrac{3x}{80}$ = $\dfrac{9}{30}$

$\Rightarrow $  x = $\dfrac{9\times 80}{30 \times 3}$

$\Rightarrow $  x =8

Now, put x=8 in eq. (i), we get

$\dfrac{8}{10}$ = t+ $\dfrac{8}{60}$

$\Rightarrow $ $\dfrac{8}{10}$ - $\dfrac{2}{15}$= t

$\Rightarrow $ $\dfrac{24-4}{30}$ = t

$\Rightarrow $ $\dfrac{20}{30}$ = t $\Rightarrow $ t=$\dfrac{2}{3}$

91. Match each of the entries in Column I with the appropriate entry in Column II.

Ans:

92. There are 20 grams of protein in 75 grams of salted fish. How many grams of protein is in 225 gm of that fish?

Ans: 75 gm fish holds protein = 20gm

1 gm of fish will hold = $\dfrac{20}{75}$

225 gm of fish will hold = $\dfrac{20}{75}\times $ 225=60gm

93. Ms. Anita has to drive from Jhareda to Ganwari. She measures a distance of 3.5 cm between these villages on the map. What is the actual distance between the villages if the map scale is 1 cm = 10 km?

Ans: Distance between jhareda to ganwari in the map = 3.5cm

Given scale 1cm = 10km

So actual distance between the villages = 35×10=35 km

94. A water tank casts a shadow 21 m long. A tree of height 9.5 m casts a shadow 8 m long at the same time. The lengths of the shadows are directly proportional to their heights. Find the height of the tank.

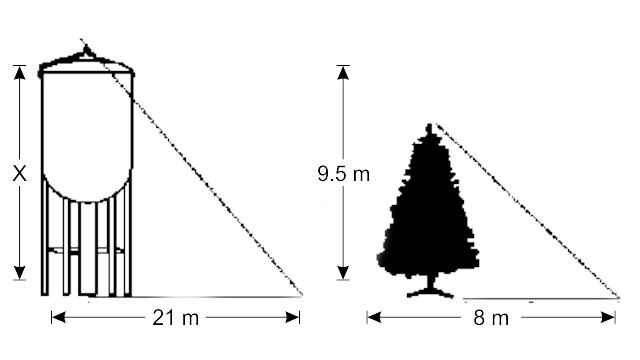
Ans: Height of the tree = 9.5cm

Shadow of the tree = 8cm

The shadows are directly proportional then

95. The table shows the time four elevators take to travel various distances. Find which elevator is fastest and which is slowest.

How much distance will be traveled by elevators B and C separately in 140 sec? Who traveled more and by how much?

Ans: Distance covered by elevator A in 1 sec =$\dfrac{435}{29}$ =15m

Distance covered by elevator B in 1 sec=$\dfrac{448}{28}$ =16m

Distance covered by elevator C in 1 sec = $\dfrac{130}{10}$ =13m

Therefore, Elevator C is slowest.

Distance covered by elevator B in 140s = 140×16=2240m

Distance covered by elevator C in 140s= 140×13=1820m

Elevator B covers more distance than C = 2240-1820=420m

96. A volleyball court is in a rectangular shape and its dimensions are directly proportional to the dimensions of the swimming pool given below. Find the width of the pool.

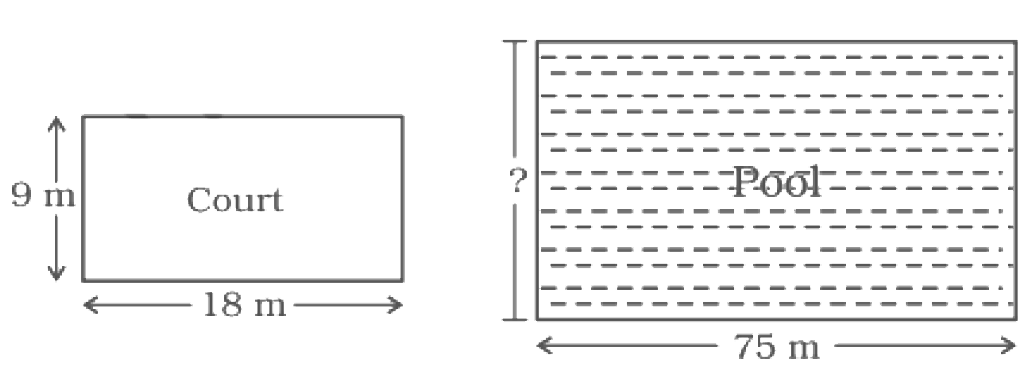
Ans: Length of the volleyball court = 18m

Breadth of volleyball court= 9m

Length of pool = 775m

Let’s assume length of the swimming pool = xm

$\dfrac{9}{18}$ = $\dfrac{x}{75}$

$\Rightarrow  x$ = $\dfrac{75 \times 9}{18}$ = $\dfrac{75 }{2}$ = 37.5m

97. A recipe for a particular type of muffins requires 1 cup of milk and 1.5 cups of chocolates. Riya has 7.5 cups of chocolates. If she is using the recipe as a guide, how many cups of milk will she need to prepare muffins?

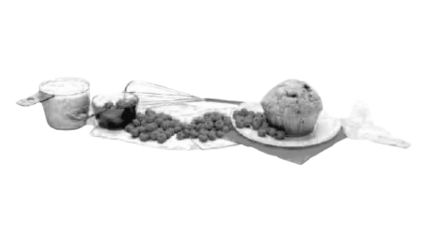
Ans: Muffin requires 1 cup of milk and 1.5 cups of chocolates

Riya has 7.5 cups of chocolates

The number of cups of milk required for 7.5 cups of chocolate = $\dfrac{7.5}{1.5}$= 5cups

98. Pattern B consists of four tiles like pattern A. Write a proportion involving red dots and blue dots in pattern A and B. Are they in direct proportion? If yes, write the constant of proportion.

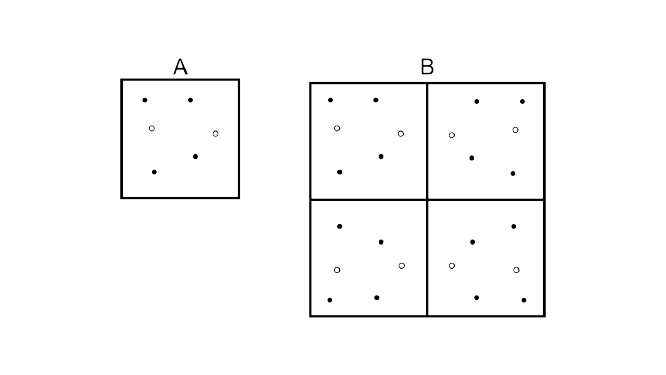
Ans: No. Of red dots = 4

No. Of blue dots = 2

Pattern B consists of four tiles like pattern A

Pattern A×4=Pattern B

Proportion of pattern =$\dfrac{2}{6}$ = $\dfrac{1}{3}$

Proportion of red dots and blue dots in pattern B =$\dfrac{8}{32}$=$\dfrac{1}{4}$

99. A bowler throws a cricket ball at a speed of 120 km/h. How long does this ball take to travel a distance of 20 meters to reach the batsman?

Ans: Speed of the cricket ball = 120km/hr = $\dfrac{120 \times 1000}{60}$ =2000m / min

100. The variable x is inversely proportional to y. If x increases by p%, then by what percent will y decrease?

Ans: xy = k(constant)

The variable x is inversely proportional to y.

If an increase causes a decrease in y and vice-a-versa this is called the inverse proportion.

101. Here is a keyboard of a harmonium:

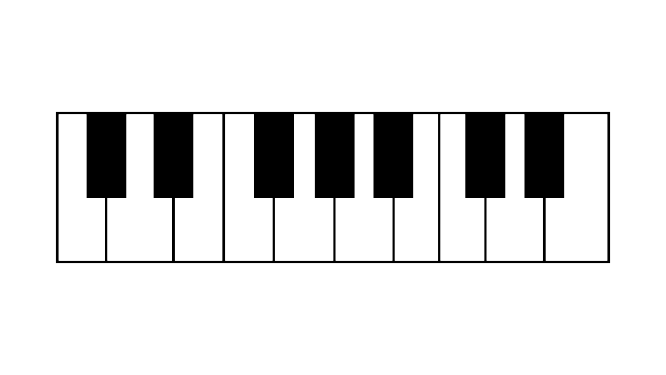
(a) Find the ratio of white keys to black keys on the keyboard.

Ans: Total no. Of keys = 7

No of white keys = 10

Their ratio = $\dfrac{10}{7}$

(b) What is the ratio of black keys to all keys on the given keyboard.

Ans: No of all keyboard = 10+7=17

Ration of black keys to all keys = $\dfrac{7}{17}$

(c) This pattern of keys is repeated on larger keyboards. How many black keys would you expect to find on a keyboard with 14 such patterns?

Ans: Black keys in 1 keyboard = 7

Black keys in 14 such keyboards = 14×7=98keys

102. The following table shows the distance traveled by one of the new eco-friendly energy-efficient cars traveled on gas.

Which type of properties is indicated by the table? How much distance will be covered by the car in 8 liters of gas?

Ans: This table describes the relation between liters of gas and the distance covered is direct proportional.

The car can cover in 8l of gas = 8×15=120km

103. Kritika is following this recipe for bread. She realizes her sister used most sugar syrup for her breakfast. Kritika has only $\dfrac{1}{6}$cup of syrup, so she decides to make a small size of bread. How much of each ingredient shall she use? Bread recipe 1 cup quick cooking oats 2 cups bread flour $\dfrac{1}{3}$ cup sugar syrup 1 tablespoon cooking oil 1$\dfrac{1}{3}$ cups water 3 tablespoons yeast 1 teaspoon salt.

Ans: Remaining sugar = $\dfrac{1}{6}$

Used sugar = 1- $\dfrac{1}{6}$ = $\dfrac{5}{6}$

Sugar syrup needed for 1 piece of bread = $\dfrac{1}{3}$

New portion of the ingredients will be =$\dfrac{1}{2}$

New recipe will look like as follows

$\dfrac{1}{2}$ cup quick cooking oats 1 cup bread flour

$\dfrac{1}{6}$ cup sugar syrup$ \dfrac{1}{2}$  cup sugar syrup

$\dfrac{3}{2}$ tablespoon $\dfrac{2}{3}$  yeast cup water

$\dfrac{1}{2}$ tablespoon salt‘

104. Many schools have a recommended students-teacher ratio as 35:1. Next year, the school expects an increase in enrolment by 280 students. How many new teachers will they have to appoint to maintain the students-teacher ratio?

Ans: Ratio of students and teacher = 35:1

This implies that for every 35 students 1 teacher is necessary

Total number of teachers required for 280 students =$\dfrac{280}{35}$ teachers

105. Kusum always forgets how to convert miles to kilometers and back again. However she remembers that her car’s speedometer shows both miles and kilometers. She knows that traveling 50 miles per hour is the same as traveling 80 kilometers per hour. To cover a distance of 200 km, how many miles Kusum would have to go?

Ans: 50 miles/hour = 80 km/hour

1 km = $\dfrac{50}{80}$  = $\dfrac{5}{8}$ miles

To cover a distance of 200 km = $\dfrac{5}{8}$ $\times $ 200 = 125 miles

106. The students of Anju’s class sold posters to raise money. Anju wanted to create a ratio for finding the amount of money her class would make for different numbers of posters sold. She knew they could raise Rs 250 for every 60 posters sold

(a) How much money would Anju’s class make for selling 102 posters?

Ans: 60 posters help Anju’s class to raise =Rs 250

1 poster will help= $\dfrac{250}{60}$ = Rs $\dfrac{25}{6}$

By selling 102 posters they collect = $\dfrac{25}{6}$ $\times $ 102 = 17$\times $25= Rs 425

(b) Could Anju’s class raise exactly Rs 2,000? If so, how many posters would they need to sell? If not, why?

Ans: On selling 1 poster anju’s class make =Rs $\dfrac{25}{6}$

To raise 2000 they need to sell = $\dfrac{25}{6}$ $\times $2000= 480 poster

Direct and Inverse Proportions - Chapter 10 of Class 8

In Direct proportions, values of two or more variables depend on each other. If one variable increases or decreases, it will equally affect the other quantity. And the opposite happens in Inverse Proportions, If one quantity increases then the other one has to go down and vice-versa. 

In this chapter, students are familiarized with the concept of Direct and Inverse Proportions or relations. The chapter is not that big and includes only two exercises. And it covers 8 marks in the examinations.

Direct Proportion or Relation

The student will get to know the definition of Direct Proportion and conditions needed to be fulfilled to identify if two quantities are in Direct relations.

Let assume x and y are two variable, and they can said to be in Direct proportion, only if they met these certain conditions:

• If x decreases, y decreases.

• If x increases, y increases.

• x/y = K or x*y = C, Where K and C are constants.

• x1/y1 = x2/y2, where y1 is the value of y at x1 , and the same is true for y2.

We, represent x is proportional to y, as such y ∝ x. A real life example of Direct relation can be as if the more fuel put in a car, the more distance the car will cover

Inverse Proportion or Relations

The student will get to know the definition of Inverse Proportion and conditions needed to be fulfilled to identify if two quantities are in Inverse relations.

Let assume x and y are two variable, and they can said to be in Inverse Proportion, only if they met these certain conditions:

• If x decreases, y Increases.

• If x increases, y decreases.

• x/y = K or x*y = C, Where K and C are constants.

• x1y1 = x2y2, where y1 is the value of y at x1 , and the same is true for y2.

We, represent x is proportional to y, as such y ∝ 1/x. A real-life example for Inverse Proportion can be that, if the speed of a car increases, the time taken to cover the same distance will decrease.