Question

You drive on Interstate 10 from San Antonio to Houston, half the time at 55 km/h and the other half at 90 km/h. On the way back you travel half the distance at 55 km/h and the other half at 90 km/h. What is your average speed,
(a) from San Antonio to Houston,
(b) from Houston back to San Antonio, and
(c) for the entire trip?
(d) What is your average velocity for the entire trip?
(e) Sketch X versus t for (a), assuming the motion is all in the positive x direction. Indicate how the average velocity can be found on the sketch.

Answer 1

Hint: Average speed is given by the total distance covered by total time taken to travel this distance. The total distance travelled is not zero even if the object returns back to its starting position, the net displacement is zero and hence so is the average velocity of the round trip.

Complete step by step answer:
Consider the Interstate 10 travels from San Antonio to Houston as shown in the figure below, let the distance between San Antonio and Houston be D and time taken be t.

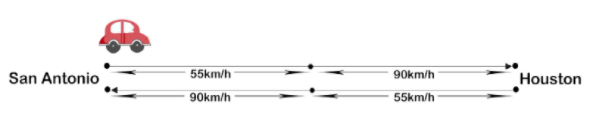
(a) Average speed from San Antonio to Houston,
Half the distance is traveled at the speed of 55km/h and half by 90km/h while going from San Antonio to Houston.

So, the total distance is given by,
$D=\dfrac{55}{\dfrac{t}{2}}+\dfrac{90}{\dfrac{t}{2}}=(\dfrac{55t}{2}+\dfrac{90t}{2})$ ….(i)

Therefore, average speed is, putting D from equation (i) we get,
${{S}_{1}}=\dfrac{D}{t}=\dfrac{(\dfrac{55t}{2}+\dfrac{90t}{2})}{t}=72.5$ km/h

(b) Average speed from Houston back to San Antonio,
Half the distance is traveled at the speed of 90km/h and half by 55km/h while going from Houston back to San Antonio.

So, the total time is given by,
$t=\dfrac{\dfrac{D}{2}}{90}+\dfrac{\dfrac{D}{2}}{55}=\dfrac{D}{180}+\dfrac{D}{110}$ ….(ii)

Therefore, average speed is, putting t from equation (ii) we get,
${{S}_{2}}=\dfrac{D}{t}=\dfrac{D}{\dfrac{D}{180}+\dfrac{D}{110}}=68.3$ km/h

(c) Average speed for the entire trip,
In returning to San Antonio, the total distance travelled from the start of the journey is 2D.
The total time T,
$T=\dfrac{D}{72.5}+\dfrac{D}{68.3}$ ….(iii)

Therefore, average speed is, putting t from equation (iii) we get,
${{S}_{av}}=\dfrac{2D}{\dfrac{D}{72.5}+\dfrac{D}{68.3}}=70$ km/h

(d) The average velocity for the entire trip is given by, the net displacement for entire trip by time,
${{V}_{av}}=0$ (since, the net displacement is zero)

(e) X versus t graph for (a),
The graph below shows the distance versus time plot,

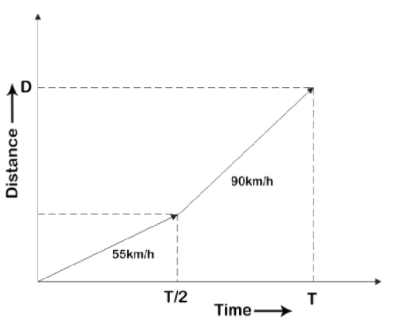
The average velocity can be calculated from the graph by joining the origin to the end of the line at (D,T) and the slope of this line will be the average velocity.

Note:
Students must not confuse between the total distance travelled and the net displacement while calculating the average speed for the entire trip when the object returns to its starting position, the net displacement is zero but total distance is not zero.