Question

You are growing a bacterial population in a laboratory flask with a flow-through system that continuously replaces the old culture medium with a fresh medium without removing any bacteria. Which of the following graphs best predicts the growth of this population over time?

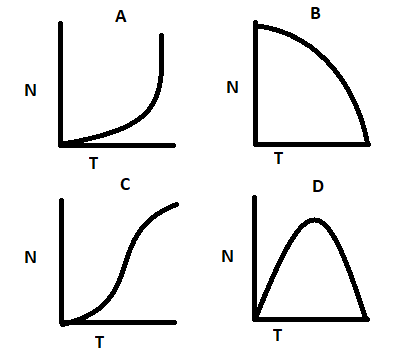
A. A
B. D
C. B
D. C

Answer 1

Hint: The process of a population's rate of growth declining as the amount of individuals in the population increases is referred to as logistic population growth. The population growth rate is a measurement of how the size of a population alters over time, and it is affected by population size, birth rate, and death rate. When a population's growth rate slows as the number of people increases, this is referred to as logistic population growth.

Complete step by step solution:
A population is a community of individuals belonging to the same species who live in the same area. The population growth rate is a measurement of how the size of a population alters over time, and it is affected by population size, birth rate, and death rate. As long as sufficient resources are available, the number of people in a population will grow over time, resulting in a positive growth rate. Most populations, however, cannot continue to grow indefinitely considering that they will eventually exhaust their supply of water, food, sunlight, space, and other resources. As these resources deplete, population growth will begin to slow. When a population's growth rate slows as the number of people increases, this is referred to as logistic population growth.

Logistic growth can also be viewed as a mathematical formula. The population growth rate is evaluated in terms of the number of people in a population (N) over time (t). The population growth rate is expressed as $\left ( \dfrac{dN}{dt} \right )$. The d simply represents change. The carrying capacity is represented by K, and the maximum per capita growth rate for a population is represented by r. The term "per capita" refers to an individual, and the per capita growth rate takes into account the number of births and lives lost in a population. The logistic growth equation indicates that K and r in a population do not change over time.
$\dfrac{dN}{dt}=rN\left ( \dfrac{K-N}{K} \right )$

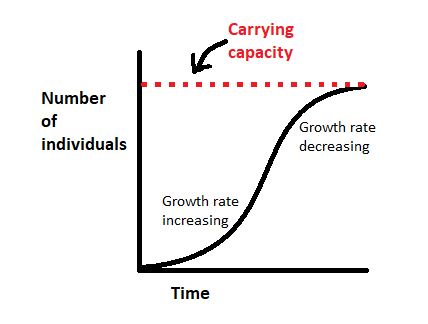
A graph of a population undergoing logistic population growth will have a distinctive S-shaped curve. When there are just a few people, the population grows slowly. When there are more people, the population grows faster. Finally, having a large population causes growth to slow since resources are limited. A population will continue to grow in logistic growth until it attains carrying capacity, which refers to the maximum number of people the environment can support.

Hence, option D is correct.

Note:
When there is not only a breeding population of significant size but also plenty of available space and other resources in the environment, new individuals are added to the population most rapidly at intermediate population sizes.