Question

Write the value of ${{\tan }^{-1}}\left( 2\sin \left( 2{{\cos }^{-1}}\dfrac{\sqrt{3}}{2} \right) \right)$ .

Answer 1

Hint: The above question is related to inverse trigonometric function and for solving the problem, you need to put the value of ${{\cos }^{-1}}\dfrac{\sqrt{3}}{2}$ . Further you need to use the values of $\sin \dfrac{\pi }{3}$ followed by the value of ${{\tan }^{-1}}\sqrt{3}$ to reach the answer.

Complete step-by-step answer:
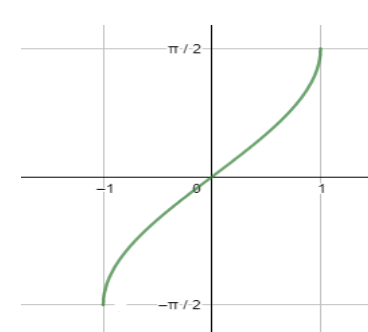
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at some of the important graphs. First, let us see the graph of ${{\sin }^{-1}}x$ .

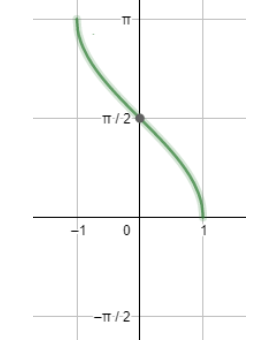
Now let us draw the graph of $co{{s}^{-1}}x$ .

Also, we will draw the graph of ${{\tan }^{-1}}x$ as well.

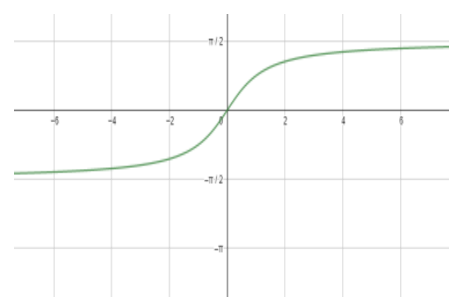
So, looking at the above graphs, we can draw the conclusion that ${{\tan }^{-1}}x$ is defined for all real values of x, i.e., the domain of the function ${{\tan }^{-1}}x$ is all real numbers while its range comes out to be $\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ . Unlike ${{\tan }^{-1}}x$ the functions $si{{n}^{-1}}x\text{ and co}{{\text{s}}^{-1}}x$ have that is defined only for $x\in [-1,1]$ .
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
${{\tan }^{-1}}\left( 2\sin \left( 2{{\cos }^{-1}}\dfrac{\sqrt{3}}{2} \right) \right)$
We know that ${{\cos }^{-1}}\dfrac{\sqrt{3}}{2}=\dfrac{\pi }{6}$ , and $\dfrac{\sqrt{3}}{2}$ also lies in the domain of ${{\cos }^{-1}}x$ . So, using this value in our expression, we get
${{\tan }^{-1}}\left( 2\sin \left( 2\times \dfrac{\pi }{6} \right) \right)={{\tan }^{-1}}\left( 2\sin \dfrac{\pi }{3} \right)$
Now, if we put the value of $\sin \dfrac{\pi }{3}$ , i.e., $\dfrac{\sqrt{3}}{2}$ , we get
${{\tan }^{-1}}\left( 2\times \dfrac{\sqrt{3}}{2} \right)$
$={{\tan }^{-1}}\sqrt{3}$
Now we know that that value of ${{\tan }^{-1}}\sqrt{3}$ is $\dfrac{\pi }{3}$ .
Therefore, the value of ${{\tan }^{-1}}\left( 2\sin \left( 2{{\cos }^{-1}}\dfrac{\sqrt{3}}{2} \right) \right)$ is equal to $\dfrac{\pi }{3}$ .

Note: Whenever dealing with such questions consisting of brackets inside another bracket, always try to start the simplification from the innermost one and move to the outer brackets one by one, as it is very difficult to visualise an operation between a number or variable and a bracket which itself has an operation occurring inside it. It is necessary that you remember the whole trigonometric table for standard angles, as they are used very often.