Question

Write the value of $\cot \left( \dfrac{\pi }{2}-2{{\cot }^{-1}}\sqrt{3} \right)$ .

Answer 1

Hint: The above question is related to inverse trigonometric function and for solving the problem you just have to put the values of ${{\cot }^{-1}}\sqrt{3}$ , which are known to us from the trigonometric table. You also have to use the value $\cot \dfrac{\pi }{6}=\sqrt{3}$ to reach the final answer.

Complete step-by-step answer:
Before starting with the solution to the above question, we will first talk about the required details of different inverse trigonometric ratios. So, we must remember that inverse trigonometric ratios are completely different from trigonometric ratios and have many constraints related to their range and domain. So, to understand these constraints and the behaviour of inverse trigonometric functions, let us look at a graph of ${{\cot }^{-1}}x$ .

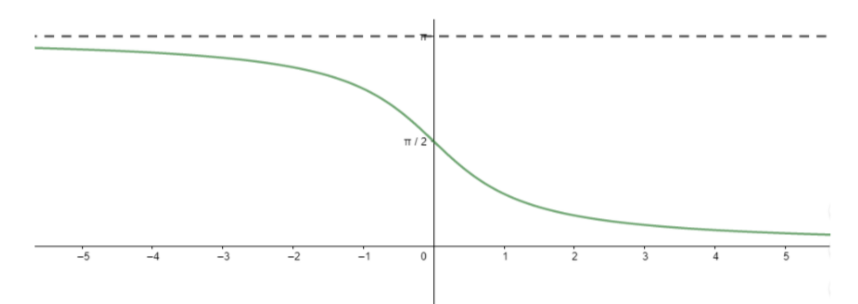
So, looking at the above graphs, we can draw the conclusion that ${{\cot }^{-1}}x$ is defined for all real values of x, i.e., the domain of the function ${{\cot }^{-1}}x$ is all real numbers while its range comes out to be $\left( 0,\pi \right)$ .
Now moving to the solution to the above question, we will start with the simplification of the expression given in the question.
$\cot \left( \dfrac{\pi }{2}-2{{\cot }^{-1}}\sqrt{3} \right)$
We know that ${{\cot }^{-1}}\sqrt{3}=\dfrac{\pi }{6}$ , and $\sqrt{3}$ also lies in the domain of ${{\cot }^{-1}}x$ . So, using this value in our expression, we get
$\cot \left( \dfrac{\pi }{2}-2\times \dfrac{\pi }{6} \right)=\cot \left( \dfrac{\pi }{2}-\dfrac{\pi }{3} \right)=\cot \dfrac{\pi }{6}$
Now, if we put the value of $\cot \dfrac{\pi }{6}$ , i.e., $\sqrt{3}$ , we get
$\cot \dfrac{\pi }{6}=\sqrt{3}$
Therefore, the value of $\cot \left( \dfrac{\pi }{2}-2{{\cot }^{-1}}\sqrt{3} \right)$ is equal to $\sqrt{3}$ .

Note: While dealing with inverse trigonometric functions, it is preferred to know about the domains and ranges of the different inverse trigonometric functions. For example: the domain of ${{\sin }^{-1}}x$ is $[-1,1]$ and the range is $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$ . You also need to remember the trigonometric table for solving such questions.