Question

Write the prime factorization of $98$, using factor tree method.

Answer 1

Hint:We have to find prime factorization of the given number by factor tree method.Prime factorization method is the method when dividing the given number by the first prime number $2$and continuing dividing by $2$ until you get a decimal or remainder. We will be able to find factorization by factor tree methodFinally, we get prime factors by factor tree method.

Complete step-by-step answer:
It is given that the number $98$
Now, the prime factorization of $98$ by using factor tree method
Prime factorization method is the method when dividing the given number by the first prime number which is $2$ and continuing dividing by $2$ until we get a decimal or remainder.
Then divide by $2,3,5,7,11$….etc. until the only numbers are left should be prime numbers. After getting this we write the numbers as a product of prime numbers.
Factor Tree method

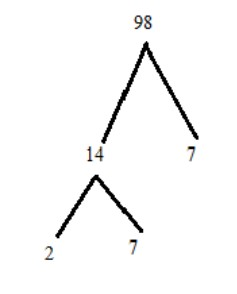
Factor is the number or algebraic expression which divides another number or expression with no remainder.
We can write $98 = 14 \times 7$(where $14$ and $7$ are factors of \[98\])
 $\therefore 98$ has two branches which contains $14$ and $7$ where $14$ is further factorized
Now \[14\] has \[2\] branches means we can write $14 = 2 \times 7$ which contains $2$ and $7$ as prime factors.
Finally, $2,7$ and $7$ do not need any further branches because it is a prime number.
We don’t need to go further.
Our Factor tree method is complete
We got all prime factors by factor tree method.
∴ $98 = 2 \times 7 \times 7$.
We got the required result.

Note:Factor of \[98\] are \[1,2,7,14,49\]
All factor pairs of 98 are combination of two factors that when multiplied together give \[98\]
They are \[\left( {1,98} \right),\left( {2,49} \right)\] and \[\left( {7,14} \right)\]
Smallest prime number is $2$(Prime numbers are those numbers which have only two factors one is $1$ and another is the number itself).