Question

Write the formula of Biot-savart law in vector form. Obtain an expression of the magnetic field on the axis of a current-carrying circular loop. Draw the necessary diagram.

Answer 1

Hint: In this problem we have to write Biot-Savart law and that too in vector form. Biot savart law helps us to find out the magnetic field due to a current carrying wire. The Biot-Savart law we know is given by \[dB=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{idl\sin }{{{r}^{2}}}\]

Complete step by step solution:
Biot-savart’s law in vector form:-
The Biot-savart’s law gives the magnetic field produced due to the current carrying segment. This segment is taken as a vector quantity known as the current element. The magnitude of the magnetic field dB at a distance r from a current-carrying element dl is found to be proportional to I and the length dl.
\[dB=\dfrac{{{\mu }_{0}}}{4\pi }\dfrac{idl\sin }{{{r}^{2}}}\]
(dl and \[{{r}^{2}}\] is vector quantity)
\[\overrightarrow{db}=\dfrac{{{\mu }_{0}}i}{4\pi }\,\,\dfrac{\overrightarrow{dl}\,\,\times \,\,\overrightarrow{r}}{{{\left| \,\overrightarrow{r\,} \right|}^{3}}}\to vector\,\,form\]
\[where\,\,\overrightarrow{a}\,\,\times \,\,\overrightarrow{b}=\,\,ab\,\,\sin \,\,\theta \]

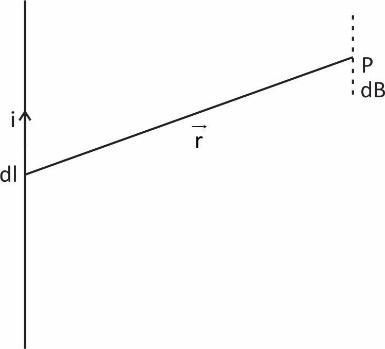
\[\left| \overrightarrow{db} \right|\,\,=\,\,\dfrac{{{\mu }_{0}}idlsi\theta }{{{r}^{2}}}\to Magnitude\]
The magnetic field on the axis of a circular current-carrying loop.

Each point on the axis is unique because the magnetic field changes the magnitude as we move further from the centre of the loop. So there’s no easy way to apply Ampere’s Law.

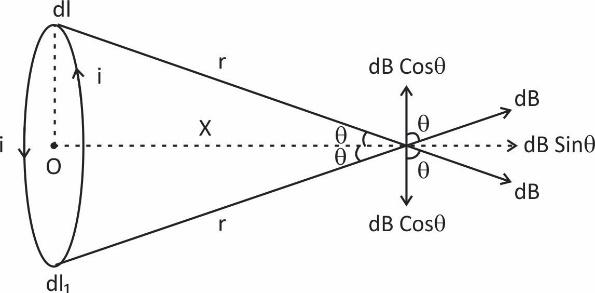
Biot Savart’s law, Magnetic field at an Aerial point P due to a current element of the ring
\[db=\dfrac{{{\mu }_{0}}}{4\pi }:\dfrac{\left( \overrightarrow{dl}\times \overrightarrow{r} \right)}{{{r}^{2}}}\]
Where \[r=\sqrt{{{R}^{2}}+{{x}^{2}}}\] (Pythagoras theorem)
\[\therefore \] We get \[B=\dfrac{{{\mu }_{0}}\,\,idl}{4\pi \,\,\left( {{R}^{2}}+{{x}^{2}} \right)}\]
We resolve dB into vertical and horizontal components. Now all the vertical components cancel out each other and so only the horizontal components survive which results in the net magnetic field at P in the horizontal direction.
Net magnetic field \[B=\int{db\,\,\operatorname{Sin}\theta }\]
\[B=\int{\dfrac{{{\mu }_{0}}idl}{4\pi \left( {{R}^{2}}+{{x}^{2}} \right)}\,\,\dfrac{R}{{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{1}{2}}}}}\]
Or \[B=\dfrac{{{\mu }_{0}}iR}{4\pi {{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{3}{2}}}}\,\,\,\,\,\int{dl}\,\,\,\left[ \sin \theta =\dfrac{R}{{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{1}{2}}}} \right]\]
Or \[B=\dfrac{{{\mu }_{0}}iR}{4\pi {{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{3}{2}}}}\left( 2\pi R \right)\]
\[\Rightarrow \,\,B=\dfrac{{{\mu }_{0}}i{{R}^{2}}}{2{{\left( {{R}^{2}}+{{x}^{2}} \right)}^{\dfrac{3}{2}}}}\]

Note: Magnetic field is maximum at centre (x = 0) and zeros at infinity \[x=\infty \]
The magnetic field is in the same direction along the axis on either side of the loop. While applying Biot-Savart law we also need to be careful in finding out the angle and that too between the current carrying element and the displacement vector up to the point where the field is to be determined.