
Write the factors of 120 as pairs.
Answer
602.1k+ views
Hint: First find the prime factors of 120 using prime factorization method, then write 120 as the product of primes. Combine the primes so that they form a multiple of two numbers to give 120. List the numbers.
Complete step-by-step answer:
The number 120 is a composite number and the factors of 120 are numbers which when multiplied with another factor, gives back 120.
The prime factors of 120 can be found using the prime factorization method. In this method, we first divide 120 by the first prime number 2 until we get a remainder. Then, we divide the number by the next prime number 3 until we get a remainder and so on with the next prime number until we get 1. Then we can represent the number 120 as the product of these prime factors.
Now, we find the prime factors of 120.
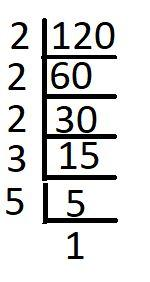
Hence, 120 can be written as follows:
\[120 = 2 \times 2 \times 2 \times 3 \times 5\]
Now, we can multiply the factors, to form pairs.
\[1 \times 120 = 120\]
\[2 \times 60 = 120\]
\[3 \times 40 = 120\]
\[4 \times 30 = 120\]
\[5 \times 24 = 120\]
\[6 \times 20 = 120\]
\[8 \times 15 = 120\]
\[10 \times 12 = 120\]
Hence, the factors of 120 in pairs are : (1, 120), (2, 60), (3, 40), (4, 30), (5, 24), (6, 20), (8, 15), and (10, 12).
Note: You can also directly write the factors in pairs without finding the prime factors. But it is to make sure that all possible pairs are listed out, we find the prime factors and then evaluate.
Complete step-by-step answer:
The number 120 is a composite number and the factors of 120 are numbers which when multiplied with another factor, gives back 120.
The prime factors of 120 can be found using the prime factorization method. In this method, we first divide 120 by the first prime number 2 until we get a remainder. Then, we divide the number by the next prime number 3 until we get a remainder and so on with the next prime number until we get 1. Then we can represent the number 120 as the product of these prime factors.
Now, we find the prime factors of 120.
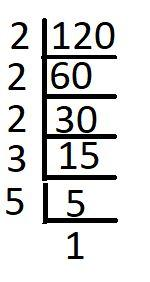
Hence, 120 can be written as follows:
\[120 = 2 \times 2 \times 2 \times 3 \times 5\]
Now, we can multiply the factors, to form pairs.
\[1 \times 120 = 120\]
\[2 \times 60 = 120\]
\[3 \times 40 = 120\]
\[4 \times 30 = 120\]
\[5 \times 24 = 120\]
\[6 \times 20 = 120\]
\[8 \times 15 = 120\]
\[10 \times 12 = 120\]
Hence, the factors of 120 in pairs are : (1, 120), (2, 60), (3, 40), (4, 30), (5, 24), (6, 20), (8, 15), and (10, 12).
Note: You can also directly write the factors in pairs without finding the prime factors. But it is to make sure that all possible pairs are listed out, we find the prime factors and then evaluate.
Recently Updated Pages
Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is the Full Form of ISI and RAW

What is pollution? How many types of pollution? Define it




