Question

Write the expression of current in terms of time.

A. $i = {i_0}\dfrac{t}{{{t_0}}}$
B. $i = {i_0}(1 + \dfrac{t}{{{t_0}}})$
C. $i = {i_0}(\dfrac{t}{{{t_0}}} - 1)$
D. $i = {i_0}(1 - \dfrac{t}{{{t_0}}})$

Answer 1

Hint: In order to solve this question we need to understand current. So electric current is defined as the number of charges flowing in unit area and in unit interval of time. Actually when a wire is subjected to potential difference then an electric field is set up in the wire which binds the electrons to move in opposite direction hence electric current moves in direction of decreasing potential or in the direction of the electric field. Straight line equation can be written in terms of slope or tangent of angle that it makes with the x-axis.

Complete step by step answer:
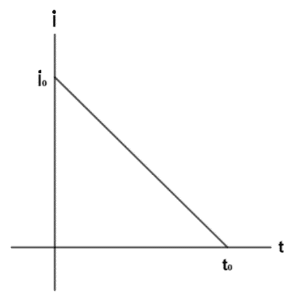
In the given figure, the curve shown is straight line having slope, “m” which is equal to, $m = \dfrac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}$ where the two points on line are $({x_1},{y_1}) = ({t_0},0)$ and $({x_2},{y_2}) = (0,{i_0})$ on putting these values we get, So slope is given as,
\[m = \dfrac{{{i_0} - 0}}{{0 - {t_0}}} = - \dfrac{{{i_0}}}{{{t_0}}}\]
Also from figure, y intercept of this straight line is, $c = {i_0}$
Since we know, standard equation of straight line having y intercept is given as, $y = mx + c$
Here, “m” is the slope of the straight line and “c” is the intercept of the straight line (the point where it intersects with the y-axis).
So putting values we get,
$y = - \dfrac{{{i_0}}}{{{t_0}}}x + {i_0}$
Since above straight line is made in “I” and “t” axis so, $y = i$ and $x = t$
So final equation is,
$i = - \dfrac{{{i_0}}}{{{t_0}}}t + {i_0}$
$\therefore i = {i_0}( - \dfrac{t}{{{t_0}}} + 1)$

The correct option is D.

Note: It should be remembered that electric current flows only due to potential difference, this fact is false rather it is not always the case, electric current can flow without the potential difference, it just requires the charge to flow from a unit area and in a unit interval of time. The slope of a line physically means how much the tangent of the angle made by the line with positive X axis in anticlockwise manner.