Question

Write the decimal expansion of \[\dfrac{1}{{14}}\] up to \[7\] decimal places.

Answer 1

Hint:The decimal expansion of a number is its representation in base \[ 10\] (that is in the decimal system). In this system, each "decimal place" consists of a digit 0-9 arranged such that each digit is multiplied by a power of \[10\], decreasing from left to right, and with a decimal place indicating the \[{10^0} = {1^{st}}\] place.The digits after point are similarly expressed such that each digit is multiplied by a negative power of \[10\].To find the decimal expansion of a given number we need to divide the numerator by denominator and get the quotient up to \[7\] decimal place.

Complete step-by-step answer:
The given number is \[\dfrac{1}{{14}}\]. We need to find the decimal expansion of the number up to 7 decimal places.
We have to convert a fraction to a decimal is just a division operation. So the fraction \[\dfrac{1}{{14}}\] means \[1 \div 14\].
Then we get,

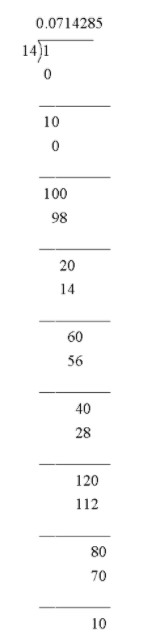
Here we see that after carrying division \[8\] times we return with a remainder \[10\] which is the dividend at the second step of division continuing after 6 steps. Thus the string \[714825\] respects in the quotient infinitely often. Thus the decimal expansion of ​\[\dfrac{1}{{14}}\] looks like \[\dfrac{1}{{14}} = 0.0714285714285....\](Here remainder is never \[0\]).
Since the number after in the \[{8^{th}}\] decimal place is \[7\](greater than \[5\]) by round of rule the \[{7^{th}}\] place digit will be \[5 + 1 = 6\].
Thus we can make it up to \[7\] decimal places,\[\dfrac{1}{{14}} = 0.0714286\]
Now, we need to express this as decimal expansion so we get,
\[0.0714286 = 0 \times {10^{ - 1}} + 7 \times {10^{ - 2}} + 1 \times {10^{ - 3}} + 4 \times {10^{ - 4}} + 2 \times {10^{ - 5}} + 8 \times {10^{ - 6}} + 6 \times {10^{ - 6}}\]

Note:A decimal representation of a non-negative real number r is an expression in the form of a series, traditionally written as a sum
\[r = \sum\limits_{i = 0}^\infty {\dfrac{{{a_i}}}{{{{10}^i}}}} \]
where \[{a_0}\] is a nonnegative integer, and \[{a_1},{a_{2,}}........\] are integers satisfying \[0 \leqslant {a_i} \leqslant 9\] , called the digits of the decimal representation.
Rules of rounding a number up to a certain decimal places:
If the number you are rounding is followed by \[5,{\text{ }}6,{\text{ }}7,{\text{ }}8,{\text{ or }}9\] round the number up.
If the number you are rounding is followed by \[0,{\text{ }}1,{\text{ }}2,{\text{ }}3,{\text{ or }}4\] leave the rounded number as it is.