Question

Write number of edges, faces and vertices of cube, cuboid, cone, cylinder, sphere, triangular pyramid, rectangular and prism.

Answer 1

Hint: The question is to write the number of edge faces, vertices of given geometrical figures. Face is the flat surface of any geometrical figure. An edge is where the two faces meet and vertex is a corner where edges meet and the plural of vertex is called vertices and edge, face and vertices can be counted after knowing the shape of the geometrical figure.

Complete answer:
In the given question, We have to write the number of faces, edges and vertices of various geometrical figures. We will count them one after another.
Firstly, Talking about cube.

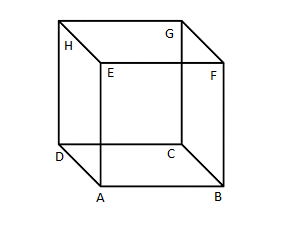
Cube is a three dimensional figure which is number of faces \[ = 6\left( {HEAD,{\text{ }}GFBC,{\text{ }}ABFE,{\text{ }}DCGH,{\text{ }}HEFG,{\text{ }}ABCD} \right)\]
Number of edges \[ = 12\left( {AB,{\text{ }}BC,{\text{ }}CD,{\text{ }}DA,{\text{ }}EF,{\text{ }}FG,{\text{ }}GH,{\text{ }}HE,{\text{ }}HD,{\text{ }}EA,{\text{ }}GC,{\text{ }}FB} \right)\]
Number of vertices \[\left( {A,{\text{ }}B,{\text{ }}C,{\text{ }}D,{\text{ }}E,{\text{ }}F,{\text{ }}G,{\text{ }}H} \right)\]
Now we will draw the figure of cuboid
In Cuboid,

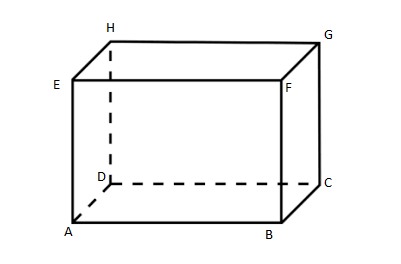
Number of faces \[ = 6\left( {HEAD,GFBC,ABFE,DCGH,HEFG,ABCD} \right)\]
Number of edges \[ = 12\left( {AB,{\text{ }}BC,{\text{ }}CD,{\text{ }}DA,{\text{ }}EF,{\text{ }}FG,{\text{ }}HG,{\text{ }}HE,{\text{ }}HD,{\text{ }}EA,{\text{ }}GC,{\text{ }}FB} \right)\]
Number of vertices \[ = 8\left( {A,{\text{ }}B,{\text{ }}C,{\text{ }}D,{\text{ }}E,{\text{ }}F,{\text{ }}G,{\text{ }}H} \right)\]
In Cone,

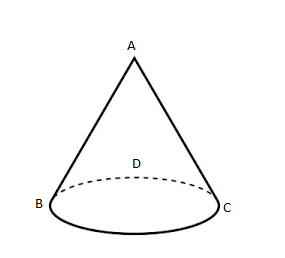
Number of faces\[ = 2\]
One is the triangular part and another is sphere part.
Number of edge \[ = 1\] edge is spherical part because both the faces are meeting there
Number of vertices \[ = 1\left( A \right)\]
In cylinder,

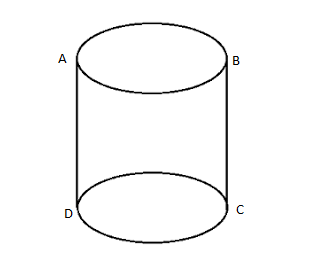
 Number of faces \[ = 3\]
One upper spherical part, second lower spherical part and third is the middle part of the spheres number of edges\[ = 2\]
Those are \[AD\] & \[BC\]
Number of vertices \[ = 0\]
Because there is no point where edges meet in sphere.

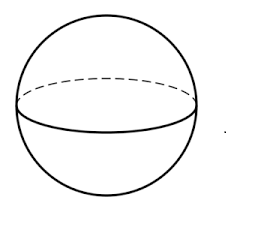
Number of faces \[ = 0\]
Because there is no face
Number of edges \[ = 0\]
Because there is no face
Number of vertices\[ = 0\]
Because there is no edge
In triangular pyramid,

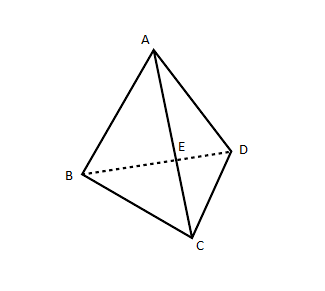
Number of faces \[ = 4\]
Because it has \[4\]sides \[ABC,{\text{ }}ACD\] and \[2\] are at its back.
Number of edges \[ = 6\] like \[AB,{\text{ }}AD\] etc.
Number of vertices \[ = 6\](\[A,{\text{ }}B,{\text{ }}C,{\text{ }}D,{\text{ }}E\] and one at its back)
In rectangular prism,

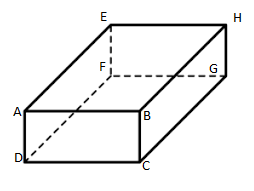
Number of faces \[ = 6\left( {ADEF,{\text{ }}BCGH,{\text{ }}EHFG,{\text{ }}ABCD,{\text{ }}DCGF,{\text{ }}ABHE} \right)\]
Number of edges \[ = 12\left( {AB,{\text{ }}BC,{\text{ }}CD,{\text{ }}AD,{\text{ }}EF,{\text{ }}FG,{\text{ }}GH,{\text{ }}HE,{\text{ }}DF,{\text{ }}AE,{\text{ }}CG,{\text{ }}BH} \right)\]
Number of vertices \[ = 8\left( {A,{\text{ }}B,{\text{ }}C,{\text{ }}D,{\text{ }}E,{\text{ }}F,{\text{ }}G,{\text{ }}H} \right)\]

Note: We have discussed edges, faces and vertices of many three dimensional geometric figures. Also these three are related to a specific formula which is known as Euler’s formula and the formula is \[F + V = E + 2,\] where F is number of faces, V is number of vertices and E is the number of edges of the given geometrical figure.