Question

Write Heron’s formula.

Answer 1

Hint: Heron’s formula is used to find the area of a triangle where the length of sides of the triangle is given. It is also known as Heron's Formula. The angle of the triangle is not necessary to calculate the area of the triangle.

Complete answer:
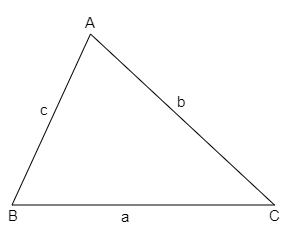
Heron’s theorem or formula was named after Heron of Alexandria who found the world of triangles are often measured in terms of the length of their sides. By deriving Heron’s formula, you'll calculate the world of a triangle without measuring the angles or the other distances. This formula is understood for its simple calculation supporting the length of three sides of a triangle.
Let say, if the length of three sides are a, b, and c, then its semi-perimeter is
$s = \dfrac{{a + b + c}}{2}$
Thus, the area is given by,
$A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)} $

Note: Let us learn how to find the area of quadrilateral using Heron’s formula here.
If ABCD is a quadrilateral, where AB||CD and AC & BD are the diagonals.

AC divides the quadrilateral ABCD into two triangles ADC and ABC.
Now we have two triangles here.
Area of quad. ABCD = Area of \[\Delta ADC\] + Area of $\Delta ABC$
So, if we all know the lengths of all sides of a quadrilateral and length of diagonal AC, then we will use Heron’s formula to seek out the entire area.
So, we will first find the area of ∆ADC and area of ∆ABC using Heron’s formula and at last, will add them to get the final value.