Question

How do you write an equation for a circle whose diameter has endpoints \[\left( { - 2,3} \right)\] and \[\left( {4, - 1} \right)\].

Answer 1

Hint: Here, we need to find the equation of the circle. First, we will use the endpoints of the diameter and the midpoint formula to find the coordinates of the centre of the circle. Then, we will use the distance formula to find the radius of the circle. Finally, we will use the coordinates of the centre, and the radius of the circle to find the equation of the circle.

Formula Used:
We will use the following formulas:
1. According to the midpoint formula, the coordinates of the mid-point of the line segment joining two points \[P\left( {{x_1},{y_1}} \right)\] and \[Q\left( {{x_2},{y_2}} \right)\] are given by \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\].
2. The distance between two points \[\left( {{x_1},{y_1}} \right)\] and \[\left( {{x_2},{y_2}} \right)\] is given by the formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \].
3. The equation of a circle is given by \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\], where \[\left( {h,k} \right)\] is the centre of the circle, and \[r\] is the radius of the circle.

Complete step-by-step solution:
Let the centre of the circle be given by the point \[B\left( {h,k} \right)\].
First, we will draw the given circle with the given diameter.

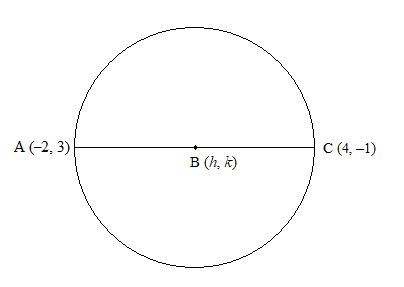
Here, A and C are the endpoints of the diameter AC, and B is the centre of the circle.
We know that the centre of a circle is the midpoint of the diameters of the same circle.
Therefore, B is the mid-point of the line segment AC.
We will use the midpoint formula to find the coordinates of the centre of the circle.
Substituting \[ - 2\] for \[{x_1}\], 4 for \[{x_2}\], 3 for \[{y_1}\], and \[ - 1\] for \[{y_2}\] in the expression \[\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)\], we get
\[\left( {h,k} \right) = \left( {\dfrac{{ - 2 + 4}}{2},\dfrac{{3 + \left( { - 1} \right)}}{2}} \right)\]
Comparing the abscissa, we get
\[h = \dfrac{{ - 2 + 4}}{2}\]
Adding the terms in the expression, we get
\[ \Rightarrow h = \dfrac{2}{2}\]
Dividing 2 by 2, we get
\[ \Rightarrow h = 1\]
Comparing the ordinates, we get
\[k = \dfrac{{3 + \left( { - 1} \right)}}{2}\]
Adding the terms in the expression, we get
\[ \Rightarrow k = \dfrac{2}{2}\]
Dividing 2 by 2, we get
\[ \Rightarrow k = 1\]
Thus, the centre of the circle is \[\left( {1,1} \right)\].
The distance between the centre of the circle and the endpoint of the diameter is the radius of the circle.
We will use the distance formula to find the radius of the circle.
Substituting \[ - 2\] for \[{x_1}\], 1 for \[{x_2}\], 3 for \[{y_1}\], 1 for \[{y_2}\], and \[AB\] for \[d\] in the distance formula \[d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \], we get
\[ \Rightarrow AB = \sqrt {{{\left[ {1 - \left( { - 2} \right)} \right]}^2} + {{\left( {1 - 3} \right)}^2}} \]
Simplifying the expression, we get
\[ \Rightarrow AB = \sqrt {{3^2} + {{\left( { - 2} \right)}^2}} \]
Applying the exponent on the terms, we get
\[ \Rightarrow AB = \sqrt {9 + 4} \]
Adding the terms, we get
Thus, the radius of the given circle is of length \[\sqrt {13} \] units.
Finally, we will use the radius and centre of the circle to find the equation of the circle.
Substituting 1 for \[h\], 1 for \[k\], and \[\sqrt {13} \] for \[r\] in the equation \[{\left( {x - h} \right)^2} + {\left( {y - k} \right)^2} = {r^2}\], we get
\[ \Rightarrow {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = {\left( {\sqrt {13} } \right)^2}\]
The square of the difference of two numbers is given by the algebraic identity \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\].
Simplifying the expression, we get
\[ \Rightarrow {x^2} + 1 - 2x + {y^2} + 1 - 2y = 13\]
Combining the like terms in the expression, we get
\[ \Rightarrow {x^2} + {y^2} - 2x - 2y + 2 = 13\]
Subtracting 2 from both sides of the equation, we get
\[ \Rightarrow {x^2} + {y^2} - 2x - 2y = 11\]

Therefore, we get the equation of the given circle as \[{x^2} + {y^2} - 2x - 2y = 11\].

Note:
We used the terms ‘abscissa’ and ‘ordinate’ in the solution. The abscissa of a point \[\left( {x,y} \right)\] is \[x\], and the ordinate of a point \[\left( {x,y} \right)\] is \[y\].
The midpoint formula is derived from the section formula. According to the section formula, the coordinates of a point dividing the line segment joining two points \[P\left( {{x_1},{y_1}} \right)\] and \[Q\left( {{x_2},{y_2}} \right)\] in the ratio \[m:n\], are given by \[\left( {\dfrac{{m{x_1} + n{x_2}}}{{m + n}},\dfrac{{m{y_1} + n{y_2}}}{{m + n}}} \right)\]. If a point divides a line segment joining two points in the ratio 1: 1, then that point is the midpoint of the line segment.