Question

Would the image of an object be the same if we put it in front of a convex mirror and in front of a diverging lens, if they have the same focal length? If not, what would be the differences? (Distance of the object is the same in both conditions)

Answer 1

Hint: In order to solve this question, we will first use mirror equation and will find the nature of image formed by convex mirror and then we will use lens equation to find nature of image formed by diverging lens which is concave lens and then will figure out the differences.

Formula used:
The mirror equation is written as,
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
where $f, v, u$ represents focal length, image distance, object distances from the mirror.
The Lens equation is written as,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
where $f, v, u$ represents focal length, image distance, object distances from the lens.

Complete step by step answer:
We have given that, object distance and focal length is same for both convex mirror as well as concave lens. Let us find the nature of the image due to the convex mirror first using appropriate sign conventions.
$f = + f$ focal length of convex mirror. In diagram PF represents focal length
$u = - u$ negative object distance for convex mirror.

In the diagram AP represents object O distance.

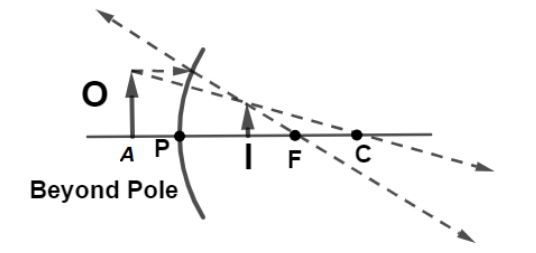
let v be the position of image as shown in diagram as distance PI then using formula, $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ we get,
$\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$
$v = \dfrac{{f + u}}{{fu}}$ so, here v is positive, it means the image is formed behind the mirror and when image formed behind the mirror it's always erect.Hence, image formed due to convex mirror is behind the mirror, virtual and erect in nature.

Now, Let us find the nature of the image due to concave lenses using appropriate sign conventions.
$f = - f$ focal length of concave lens is negative.
$u = - u$ negative object distance for concave lens.
In the diagram PA represents object O.

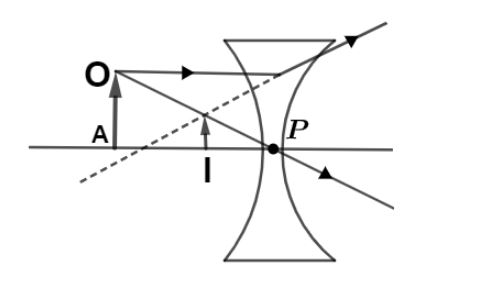
let v be the position of image represented by PI in diagram then using formula $\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}$ we get,
$ - \dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
$\therefore v = - \dfrac{{(f + u)}}{{fu}}$
so, here $v$ is negative which shows the image is formed at the same side of the object.

Hence, the basic difference in the image formation due to convex mirror and concave lens (diverging lens) is that image formed by convex mirror is formed behind the mirror but in concave lens, image is formed on the same side of the object.

Note: It should be remembered that, while putting the values of image, object distances and focal length in mirror formula and lens equation, the sign conventions are necessary to remember such that, distances left to the pole are negative while right to the pole of mirror is positive and focal length of diverging lens is negative while its positive for converging lens.