Question

How much work is required to set up the arrangement of the belowfigure if q = 2.30 pC, a = 64.0 cm, and the particles are initially infinitely far apart and at rest?

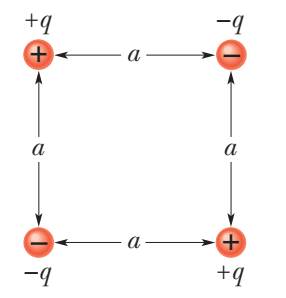
Answer 1

Hint: The work done in bringing charge from an infinity to a certain point needs a maximum amount of potential energy. The work depends on the force between the two charges and the distance between them. This will help you in answering this question.

Complete answer:
In the following diagram, the charges are labelled:

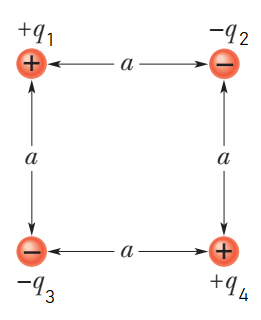
The distance between the charges ${{q}_{1}}$and ${{q}_{4}}$is $\sqrt{2}a$. Similarly, the distance between the charges ${{q}_{3}}$and ${{q}_{2}}$is $\sqrt{2}a$.
Thus the work done is the potential energy between the charges.
${{U}_{1}}$ is the potential energy between the charges ${{q}_{1}}$and ${{q}_{2}}$.
${{U}_{2}}$ is the potential energy between the charges ${{q}_{1}}$and ${{q}_{3}}$.
${{U}_{3}}$ is the potential energy between the charges ${{q}_{4}}$and ${{q}_{2}}$.
${{U}_{4}}$ is the potential energy between the charges ${{q}_{3}}$and ${{q}_{4}}$.
${{U}_{5}}$ is the potential energy between the charges ${{q}_{1}}$and ${{q}_{4}}$.
${{U}_{6}}$ is the potential energy between the charges ${{q}_{3}}$and ${{q}_{2}}$.
Here, ${{q}_{1}}={{q}_{2}}={{q}_{3}}={{q}_{4}}={{q}_{5}}={{q}_{6}}=q$
Thus, the total work done is,
$W={{U}_{1}}+{{U}_{2}}+{{U}_{3}}+{{U}_{4}}+{{U}_{5}}+{{U}_{6}}........(i)$
${{U}_{1}}={{U}_{2}}={{U}_{3}}={{U}_{4}}=\dfrac{-k{{q}^{2}}}{a}..........(ii)$
Where $k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
${{U}_{5}}={{U}_{6}}=\dfrac{k{{q}^{2}}}{a\sqrt{2}}...........(iii)$
From (i), (ii) and (iii), we get,
$\begin{align}
  & W=\dfrac{-k{{q}^{2}}}{a}+\dfrac{-k{{q}^{2}}}{a}+\dfrac{-k{{q}^{2}}}{a}+\dfrac{-k{{q}^{2}}}{a}+\dfrac{k{{q}^{2}}}{a\sqrt{2}}+\dfrac{k{{q}^{2}}}{a\sqrt{2}} \\
 & W=\dfrac{-4k{{q}^{2}}}{a}+\dfrac{2k{{q}^{2}}}{a\sqrt{2}} \\
 & W=\dfrac{-4k{{q}^{2}}}{a}+\dfrac{\sqrt{2}k{{q}^{2}}}{a} \\
 & W=\dfrac{k{{q}^{2}}(\sqrt{2}-4)}{a} \\
\end{align}$
By substituting the value, we get,
$\begin{align}
  & W=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\times {{(2.30\times {{10}^{-12}})}^{2}}\times \dfrac{1}{64\times {{10}^{-2}}}\times (\sqrt{2}-4) \\
 & W=-1.92\times {{10}^{-13}}J \\
\end{align}$

The work done to set up the experiment will be $-1.92\times {{10}^{-13}}J.$

Note:
The potential energy depends on the sign of the charge too. Though the value of the work done is negative which is absurd since it is a scalar quantity. The work done comes out to be negative because it is against the electrostatic force.