Question

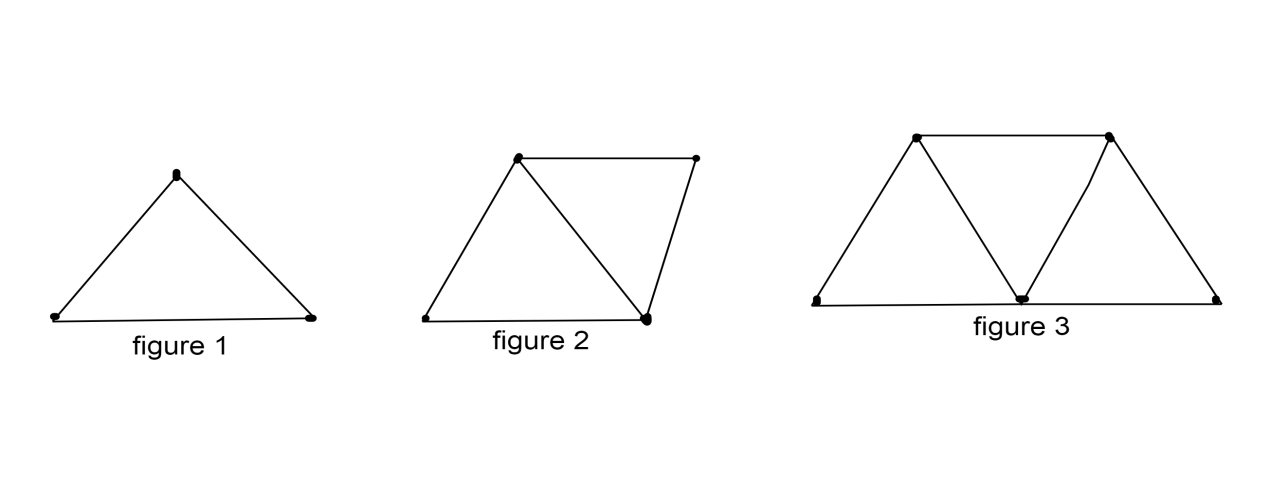
With the help of matchsticks, Zalak prepared a pattern as shown below. What will be the serial number when $97$ matchsticks are used?

A) Figure $32$
B) Figure $95$
C) Figure $49$
D) Figure $48$

Answer 1

Hint: We can see a pattern in the number of matchsticks in the figures. Identifying that pattern we can find the number of matchsticks in any of these figures.

Complete step by step solution:
Here we are given three figures on the pattern that Zalak had made.
Figure $1$ has three matchsticks, figure $2$ has five matchsticks and figure $3$ has seven matchsticks.
We can observe that the number of matchsticks increased in each stage is two.
Therefore next figures have matchsticks $9,11,13,...$
We can make a relation between the serial number of the figure and number of matchsticks in the figure.
$
  1 \to 3 = 3 \\
  2 \to 5 = 3 + 2 \\
  3 \to 7 = 3 + 2 + 2 \\
  4 \to 9 = 3 + 2 + 2 + 2 \\
 $
So in general we can say if $n$ is the serial number, then the number of matchsticks used is $3 + (n - 1)2$.
Putting $n = 1 \Rightarrow 3 + (n - 1)2 = 3 + (1 - 1)2 = 3 + 0 = 3$
$n = 2 \Rightarrow 3 + (n - 1)2 = 3 + (2 - 1)2 = 3 + 2 = 5$ and so on.
So we have to find the serial number when there are $97$ matchsticks.
That is we have to find the value of $n$, when $3 + (n - 1)2 = 97$.
$3 + (n - 1)2 = 97 \Rightarrow 3 + 2n - 2 = 97$
Rearranging the terms we get,
$2n + 1 = 97$
Subtracting $1$ from both sides we get,
$2n + 1 - 1 = 97 - 1$
$ \Rightarrow 2n = 96$
Dividing both sides by $2$ we get,
$n = \dfrac{{96}}{2} = 48$
Hence the serial number of the figure having $97$ matchsticks is $48$.

So the answer is option D.

Note: We can also use the concept of Arithmetic sequence to solve this problem. Since in each figure the number of matchsticks is two more than the previous one, this can be considered as an arithmetic sequence with first term $3$ and common difference $2$.