Question

With the help of Kirchhoff’s Law explain the Wheatstone’s bridge principle.

Answer 1

Hint: The two rules of Kirchhoff are as follows: First rule states that the sum of all currents entering a junction must be equal to the sum of all currents leaving the junction.Kirchhoff’s second rule is also known as the loop rule, it states that the algebraic sum of all potential around any closed circuit should be zero. Construct the wheatstone’s bridge and apply any one of Kirchhoff's laws.

Complete step by step answer:
Now, let us apply Kirchhoff’s rule, it can be mathematically represented as:
$\Sigma {\rm I} = 0$
Here $\Sigma {\rm I}$ is the sum of current entering the junction and leaving the junction.
Kirchhoff’s second rule can be expressed as:
$\Sigma {\rm I}R = \Sigma {\rm E}$
Here $\Sigma R$ denotes the resistance at the junction and $\Sigma {\rm E}$ denotes the emf at the junction.
The circuit diagram for Wheatstone bridge is given below:

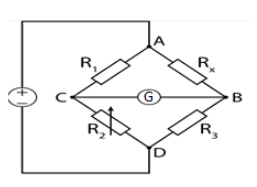
G depicts a galvanometer and it is used to measure the current flowing across two any points.${R_1},{R_2},{R_{3\,}}\,and\,{R_x}$ are the resistors connected as shown in the above diagram.The resistors are connected across the points C and B as shown.When the current is flown through the circuit and the galvanometer does not give any deflection, then the bridge is balanced. For balanced bridge we must have the condition as:
 $\dfrac{{{R_x}}}{{{R_3}}} = \dfrac{{{R_1}}}{{{R_2}}}$

Let us assume, the total current flowing in the circuit is $I$ ​. This current is divided into two parts ${i_1}$​ and ${i_2}$​ which is flowing through ${R_x}\,,{R_3}\,and\,{R_{1\,}},{R_2}$ .Now, the galvanometer shows zero deflection if the Wheatstone is balanced, that is the potential of B and C will be equal.In the closed circuit ABCD using Kirchhoff’s second law we can have:
$ \Rightarrow {i_1}{R_1} - {i_2}{R_x} = 0$
$ \Rightarrow {i_1}{R_1} = {i_2}{R_x}$ --equation 1
And
${i_1}{R_2} - {i_2}{R_3} = 0$
$ \Rightarrow {i_1}{R_2} = {i_2}{R_3}$ --equation 2
Dividing equation $1$​ by equation $2$​ , we will have
$\dfrac{{{i_1}{R_1}}}{{{i_1}{R_2}}} = \dfrac{{{i_2}{R_x}}}{{{i_2}{R_3}}}$
$ \Rightarrow \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{R_x}}}{{{R_3}}}$
Which is the required condition for Wheatstone’s bridge to be balanced.

Note: Do remember that there are two rules of Kirchhoff’s law.Both the rules can be used to prove the condition for balanced Wheatstone.Kirchhoff’s laws are used to study various types of circuits whether simple or complex circuits.The advantage of balanced wheat stone bridge is that the bridge resistance, which has no current, can be removed out of the circuit. Then the circuit resistances will be in simple series and parallel connection.