Question

While driving around a curve of radius 17.32 m, an engineer notes that a pendulum in his car hangs at an angle of \[30{}^\circ \]to the vertical. The speed of the car is
\[\begin{align}
  & A.\,10{m}/{s}\; \\
 & B.\,15{m}/{s}\; \\
 & C.\,5{m}/{s}\; \\
 & D.\,6.7{m}/{s}\; \\
\end{align}\]

Answer 1

Hint: We have to consider the vertical and the horizontal components working on the pendulum, as the pendulum makes an angle. Then, we have to divide the vertical and the horizontal components working on the pendulum to find the expression for the speed of the car. After substituting the values in that expression, we will get the required value.

Complete step by step answer:
From the given information, we have the data as follows.
While driving around a curve of radius 17.32 m, an engineer notes that a pendulum in his car hangs at an angle of \[30{}^\circ \]to the vertical.
Consider the diagram representing the centrifugal force acting on the pendulum.

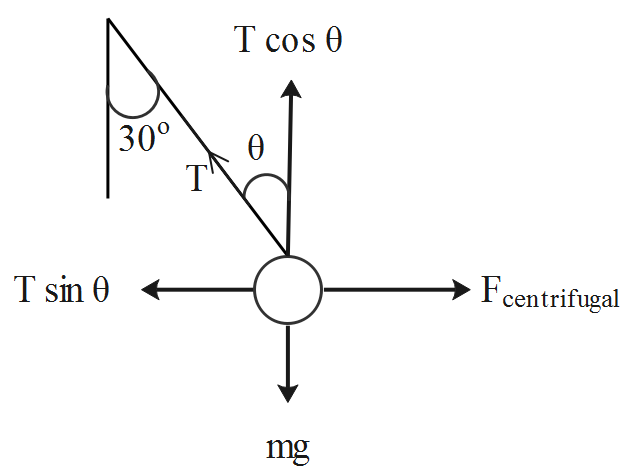
The vertical component acting on the pendulum equals the weight of the pendulum.
\[T\cos \theta =mg\]
The horizontal component acting on the pendulum equals the centrifugal force acting on the pendulum.
  \[T\sin \theta =\dfrac{m{{v}^{2}}}{r}\]
Now divide the vertical component and the horizontal component acting on the pendulum.
\[\dfrac{T\sin \theta }{T\cos \theta }=\dfrac{{}^{m{{v}^{2}}}/{}_{r}}{mg}\]
Cancelling out the common terms, we get,
\[\tan \theta =\dfrac{{{v}^{2}}}{rg}\]
Represent the above equation in terms of the speed of the car.
\[\therefore v=\sqrt{rg\tan \theta }\]
Here r equals the radius of the curve, g equals the acceleration due to gravity and \[\theta \]is the angle made by the pendulum string.
Substitute the values in the above formula.
\[v=\sqrt{17.32\times 9.8\times \tan 30{}^\circ }\]
Therefore the value of the speed of the car is,
\[v\approx 10\,{m}/{s}\;\]
So, the correct answer is “Option A”.

Note: The vertical component working on the pendulum equals the weight of the pendulum, whereas, the horizontal component working on the pendulum equals the centrifugal force acting on the pendulum.