
Which student measures the wrong equivalent resistance between A and B in the following given table:-
Student Circuit Equivalent resistance Student A
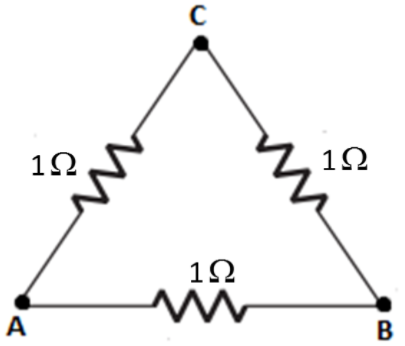
\[1\Omega \] Student B
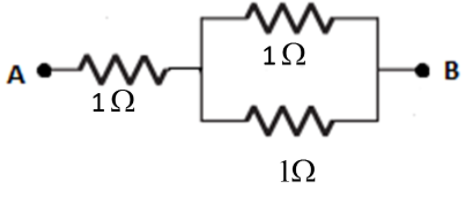
$1.5\Omega $
| Student | Circuit | Equivalent resistance |
| Student A | 
| \[1\Omega \] |
| Student B | 
| $1.5\Omega $ |
Answer
535.5k+ views
Hint: We know that there are two possible combinations of resistors. One is the series combination and the other is a parallel combination. A series combination of resistors is the same in all the resistors and the potential difference of the combination is the sum of the potential difference of each resistor. While in parallel combination potential difference is the same for each resistor but the current for the system is the sum of currents of each resistor.
Complete step-by-step solution
We know that In series connection equivalent resistance is the sum of all the individual resistances and in parallel connection the reciprocal of equivalent resistance is the sum of reciprocal of the individual resistances.
For student A, we have the value of each resistor equal to $1\Omega $. Two resistors (${{R}_{1}}$and ${{R}_{2}}$) are in series and the other one(${{R}_{3}}$) in parallel with them.
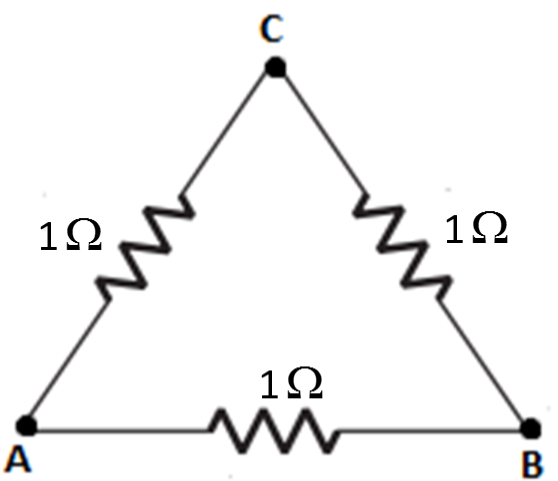
Resistance for the two resistors in series will be given as${{R}_{s}}={{R}_{1}}+{{R}_{2}}$. Therefore, it will be
${{R}_{s}}=1+1=2\Omega $.
Now, this ${{R}_{s}}=2\Omega $is in parallel with the third one
Hence using $\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{s}}}+\dfrac{1}{{{R}_{3}}}$we get
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{s}}}+\dfrac{1}{{{R}_{3}}}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1}{2}+\dfrac{1}{1}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1+2}{2}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{3}{2}$
Therefore, ${{R}_{p}}=\dfrac{2}{3}\Omega $
Hence, equivalent resistance is $0.67\Omega $
Therefore, Student A is incorrect.
For student B, we have ${{R}_{2}}$and ${{R}_{3}}$in parallel with each other and ${{R}_{1}}$in series with them.
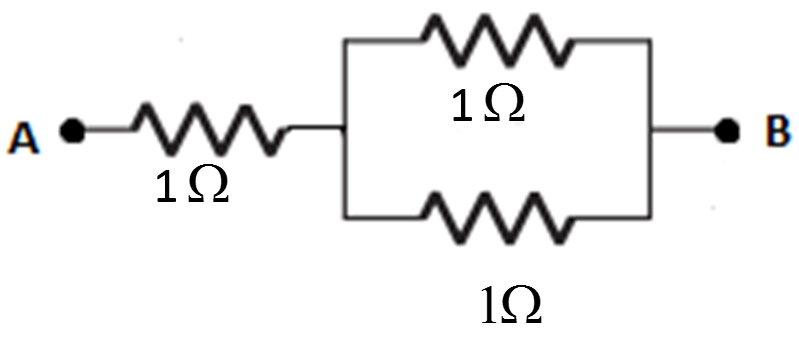
Therefore, equivalent resistance ${{R}_{eq}}$is given as follows:-
${{R}_{eq}}={{R}_{1}}+ {{R}_{s}}$
where,
$\left( \dfrac{1}{{{R}_{s}}} \right)= \left( \dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{1}{1}+\dfrac{1}{1} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{1+1}{1} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{2}{1} \right)$
Using reciprocal rule for effective resistance in parallel connection we get
$\Rightarrow {{R}_{eq}}=1+\left( \dfrac{1}{2} \right)$
$\Rightarrow {{R}_{eq}}=\dfrac{2+1}{2}$
$\Rightarrow {{R}_{eq}}=\dfrac{3}{2}$
$\Rightarrow {{R}_{eq}}=1.5\Omega $
Hence, student B is correct.
Thus, we get the final answer, student A is incorrect and student B is correct.
Note: In solving the problems related to equivalent resistance we have to identify the correct arrangements of resistances. We should not get confused between the formulae of series and parallel combinations. In a parallel combination, we have to find the reciprocal of each resistance.
Complete step-by-step solution
We know that In series connection equivalent resistance is the sum of all the individual resistances and in parallel connection the reciprocal of equivalent resistance is the sum of reciprocal of the individual resistances.
For student A, we have the value of each resistor equal to $1\Omega $. Two resistors (${{R}_{1}}$and ${{R}_{2}}$) are in series and the other one(${{R}_{3}}$) in parallel with them.

Resistance for the two resistors in series will be given as${{R}_{s}}={{R}_{1}}+{{R}_{2}}$. Therefore, it will be
${{R}_{s}}=1+1=2\Omega $.
Now, this ${{R}_{s}}=2\Omega $is in parallel with the third one
Hence using $\dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{s}}}+\dfrac{1}{{{R}_{3}}}$we get
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1}{{{R}_{s}}}+\dfrac{1}{{{R}_{3}}}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1}{2}+\dfrac{1}{1}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{1+2}{2}$
$\Rightarrow \dfrac{1}{{{R}_{p}}}=\dfrac{3}{2}$
Therefore, ${{R}_{p}}=\dfrac{2}{3}\Omega $
Hence, equivalent resistance is $0.67\Omega $
Therefore, Student A is incorrect.
For student B, we have ${{R}_{2}}$and ${{R}_{3}}$in parallel with each other and ${{R}_{1}}$in series with them.

Therefore, equivalent resistance ${{R}_{eq}}$is given as follows:-
${{R}_{eq}}={{R}_{1}}+ {{R}_{s}}$
where,
$\left( \dfrac{1}{{{R}_{s}}} \right)= \left( \dfrac{1}{{{R}_{2}}}+\dfrac{1}{{{R}_{3}}} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{1}{1}+\dfrac{1}{1} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{1+1}{1} \right)$
$\Rightarrow \left( \dfrac{1}{{{R}_{s}}} \right) = \left( \dfrac{2}{1} \right)$
Using reciprocal rule for effective resistance in parallel connection we get
$\Rightarrow {{R}_{eq}}=1+\left( \dfrac{1}{2} \right)$
$\Rightarrow {{R}_{eq}}=\dfrac{2+1}{2}$
$\Rightarrow {{R}_{eq}}=\dfrac{3}{2}$
$\Rightarrow {{R}_{eq}}=1.5\Omega $
Hence, student B is correct.
Thus, we get the final answer, student A is incorrect and student B is correct.
Note: In solving the problems related to equivalent resistance we have to identify the correct arrangements of resistances. We should not get confused between the formulae of series and parallel combinations. In a parallel combination, we have to find the reciprocal of each resistance.
Recently Updated Pages
Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Explain sex determination in humans with the help of class 12 biology CBSE




