Question

Which one of the graphs represents the function $f(x) = \dfrac{x}{x}$ , $x \ne 0$
A.

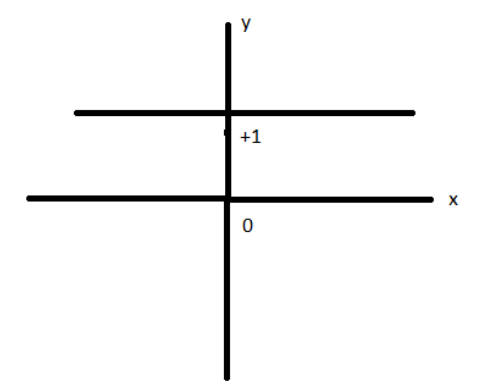
B.

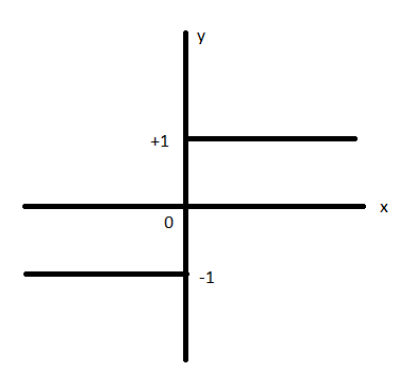
C.

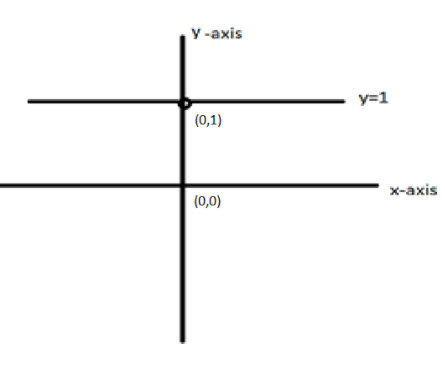
D. None of the above

Answer 1

Hint: There are two types of undefined values for fractions, they are $\dfrac{1}{0},\dfrac{0}{0}$ . When we encounter such values, we need to use the concept of limits and find out the value of the function. Sometimes we may get an infinite or undefined value as the answer even after we use limits. When we get a defined value or a bounded value, it means that there is no discontinuity in the function at that certain value of $x$.

Complete step by step answer:
In the above question, the given function is $f(x) = \dfrac{x}{x}$ , $x \ne 0$
CASE 1: When $x \ne 0$ , the function always reduces to 1 (equals to 1) because there are no undefined values anywhere.
CASE 2: But when $x = 0$, there will be a dis-continuity since $\dfrac{0}{0}$ is an undefined form.
This is a finite discontinuity and can be eliminated by using a piecewise function. Hence the correct graph would be a straight line parallel to x-axis, $y = 1$ but an open point at $x = 0$

Therefore, the correct option is C.

Note:Limits and continuity is a very important concept and is useful in solving various higher-level problems. A common mistake is to assume that $f(x) = \dfrac{x}{x}$ is always equal to 1 no matter what the value of $x$ is, not keeping in mind the undefined values. Using this concept, we can find the values of functions at certain values of $x$ where in normal substitution would give an undefined value.