Question

Which of the following statements is true for a rhombus?
A) It has only two pairs of equal sides.
B) Two of its angles are at right angles.
C) Its diagonals bisect each other at right angles.
D) It is always a square.

Answer 1

Hint: We will first draw a rhombus and see for all the options. We will then inspect all the options one by one for their truth value and see if they are correct or incorrect statements. Thus, we will have the answer.

Complete step-by-step answer:
Let us first draw a rhombus for more clarification of things.

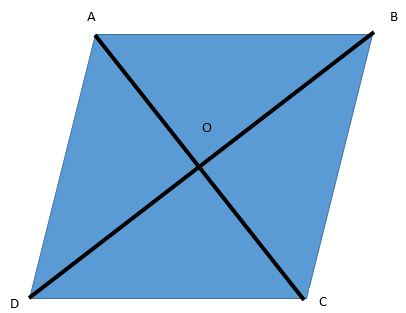
Here ABCD is the rhombus, AC and BD are the diagonals which are intersecting each other at O.
Option A: It has only two pairs of equal sides.
We know that the rhombus just lacks the condition of one angle being the right angle to form a square. Therefore, it has all the sides equal to each other.
\[\therefore \] option (A) is incorrect.
Option B: Two of its angles are at right angles.
We know that the rhombus just lacks the condition of one angle being the right angle to form a square. If it would have two of its angles as right angles, then it definitely will become a square.
\[\therefore \] option (B) is incorrect.
Option C: Its diagonals bisect each other at right angles.
We know that diagonals of a rhombus definitely do bisect each other. Now, we will see whether they bisect at right angles or not.
Consider the triangles $\vartriangle AOD$ and $\vartriangle AOB$.
AO = AO (Common)
AD = AB (Sides of a rhombus are equal to each other)
OD = OB (diagonal is bisected by other diagonal)
$\therefore \vartriangle AOD \cong \vartriangle AOB$ (By SSS congruence criterion)
[SSS congruence criterion: When all the three corresponding sides of two triangles are equal in length, the triangles are said to be congruent]
$\therefore \angle AOD = \angle AOB$ (By CPCT) ……………..(1)
[CPCT theorem states that if two or more triangles which are congruent to each other are taken then the corresponding angles and the sides of the triangles are also congruent to each other]
Now, since we see that the $\angle AOD$ and $\angle AOB$ are linear.
$ \Rightarrow \angle AOD + \angle AOB = {180^ \circ }$
Now, by using (1):
$ \Rightarrow \angle AOD = \angle AOB = {90^ \circ }$.
Similarly, we can show that all other angles where the diagonals bisect are also right angles.
$\therefore $ option (B) is correct.
Option D: It is always a square.
We know that the rhombus just lacks the condition of one angle being the right angle to form a square. Therefore, it cannot be a square
\[\therefore \] option (D) is incorrect.

\[\therefore \] The required answer is option (C).

Note: The students must know that “All the squares are rhombus because they have all the conditions to be rhombus being a square but converse is not always true.”
The students must know that the rhombus is a special kind of parallelogram where not just the opposite sides are equal in length but adjacent as well. The word “Rhombus” came from the greek work “rhombus” which means “spinning top”. A rhombus is sometimes called a “diamond”. The figure given below is of diamond: