Question

Which of the following statements is true?
a)The \[x – axis\] is a vertical line.
b)The point \[( - 2,\ 3)\] lies in the \[3^{rd}\] quadrant.
c)Origin is the point of intersection of the \[x – axis\] and \[y – axis\].
d)The point \[( - 3,\ - 4)\] lies in the \[2^{nd}\] quadrant.

Answer 1

Hint: In this question, we need to find out whether the given statement is true or false . We need to verify each statement separately whether it is true or false. We need to know the concepts of coordinate geometry to state whether the given statements are true or false.

Complete answer:
a. The \[x – axis\] is a vertical line.
The given statement is false. We know that in the coordinate plane, the horizontal line is \[x-axis\].

b.The point \[( - 2,\ 3)\] lies in the \[3^{rd}\] quadrant.
The given statement is false. In the third quadrant, \[x\] coordinate is negative and \[y\] coordinate is also negative. But in the given point, \[y\] coordinate is positive. Thus the given point lies in the fourth quadrant.

c.Origin is the point of intersection of the \[x – axis\] and \[y – axis\].

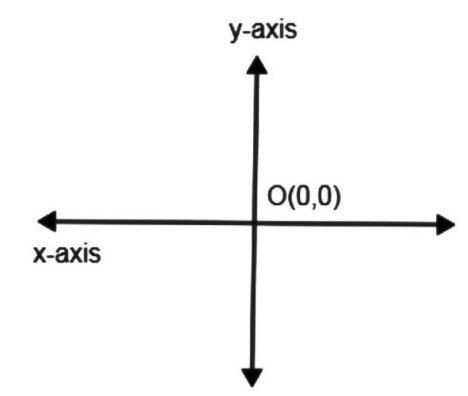
The given statement is true. Since \[x axis\] and \[y axis\] are perpendicular to each other and intersect at the point \[O\]. Thus the point of intersection of the \[x axis\] and \[y axis\] is known as the origin
d.The point \[( - 3,\ - 4)\] lies in the \[2^{nd}\] quadrant.
The given statement is false. In the second quadrant, \[x\] coordinate is negative whereas \[y\] coordinate is positive. But in the given point, \[y\] coordinate is negative. Thus the given point doesn’t lie in the second quadrant. It lies in the third quadrant.
         

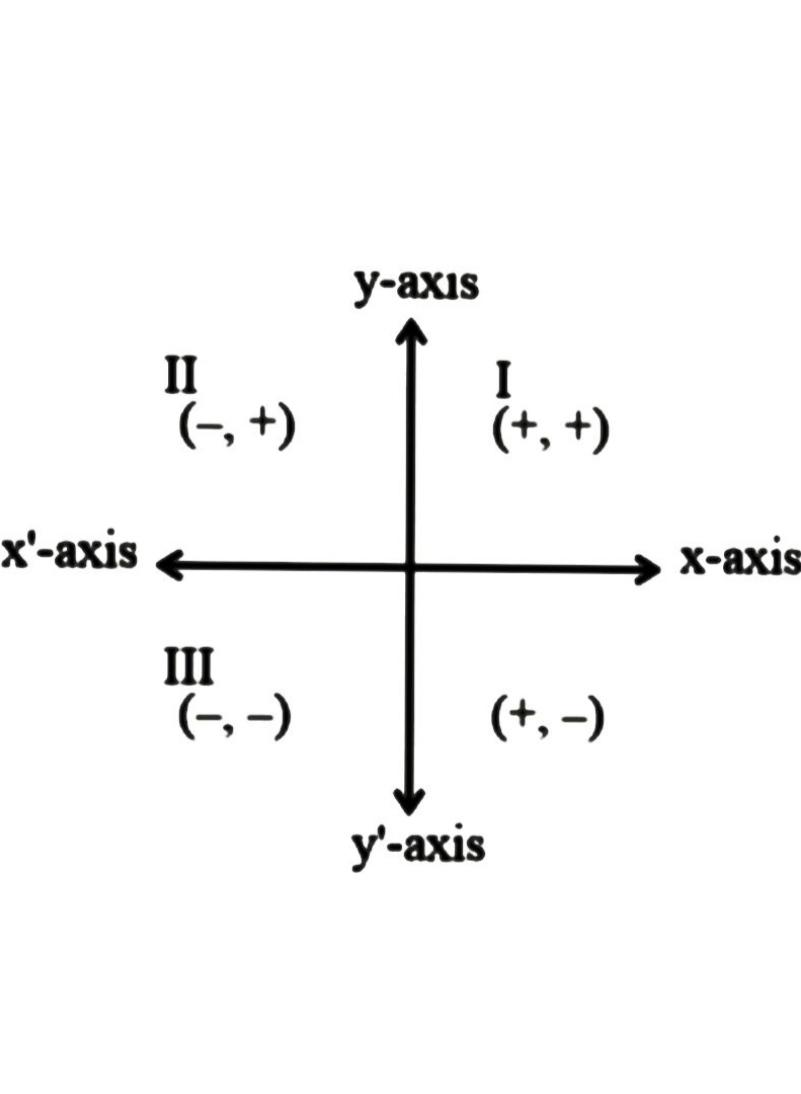
Thus we can conclude that only statement c) is true.

Note:
The concept used in this problem is coordinate geometry. Mathematically, a graph consists of two axes namely \[x\] axis and \[y\] axis. Here the horizontal axis is known as the \[x\] axis whereas the \[y\] axis is the vertical axis. When the equation is in the \[x\] axis then \[y=0\] and similarly when the equation is on the y axis then \[x=0\].