Question

Which of the following points is considered as the orthocenter of the given triangle ABC?

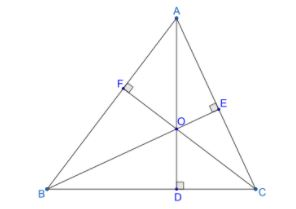
(a) D
(b) E
(c) O
(d) F

Answer 1

Hint: We start solving the problem by recalling the definition of altitudes and orthocenter of a triangle. We then check the properties of the lines AD, BE and CF from the figure and verify whether the given points are Orthocenter or not. We then check the property of the point O from the figure to verify it is Orthocenter or not.

Complete step-by-step answer:
According to the problem, we have given a triangle ABC as shown in figure. We need to find which is the orthocenter of the triangle among all the points present in the figure.
Let us redraw the figure again.

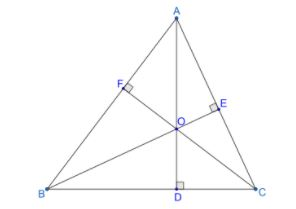
Before telling what is the orthocenter of the triangle, we first recall the definition of the orthocenter. Orthocenter is defined as the point of intersection of all the altitudes in the triangle. We know that altitude is a line which passes through the vertex of the triangle and is perpendicular to the opposite side.
From the figure, we can see that the line segment AD is passing through the vertex A and is perpendicular to the side BC. This makes line segment AD an altitude and which tells point D is not an Orthocenter.
From the figure, we can see that the line segment BE is passing through the vertex B and is perpendicular to the side AC. This makes line segment BE an altitude and which tells us point E is not an Orthocenter.
From the figure, we can see that the line segment CF is passing through the vertex C and is perpendicular to the side AB. This makes line segment CF an altitude and which tells us point F is not an Orthocenter.
From the figure, we can see that the point is formed by the line intersection of line segments AD, BE and CF which are altitudes of the triangle. We can see that the definition of orthocenter holds true for the point O.
∴ The point O is the orthocenter of the triangle.

So, the correct answer is “Option c”.

Note: We should not confuse the notation of line segments in a triangle like median, altitude and angular bisectors. We should know that the orthocenter need not pass through the midpoint of the side, it just needs to be perpendicular with the side of the triangle. Similarly, we can also expect problems involving the medians and centroid or internal angular bisectors and incenter or external angular bisectors and incenter.