Question

Which of the following pair of points lie on the same side of $ 3x-8y-7=0 $ ?
A. $ \left( 0,-1 \right) $ and $ \left( 0,0 \right) $
B. $ \left( 4,-3 \right) $ and $ \left( 0,1 \right) $
C. $ \left( -3,-4 \right) $ and $ \left( 1,2 \right) $
D. $ \left( -1,-1 \right) $ and $ \left( 3,7 \right) $

Answer 1

Hint: Change of form of the given equation will give the x-intercept and y-intercept of the line $ 3x-8y-7=0 $ . We change it to the form of $ \dfrac{x}{p}+\dfrac{y}{q}=1 $ to find the x intercept, and y intercept of the line as $ p $ and $ q $ respectively. Then we place the points on the equation to find the signs and decide their positions.

Complete step-by-step answer:
We are taking the general equation of line to understand the slope and the intercept form of the line $ 3x-8y-7=0 $ . The given equation is in the form of $ y=mx+k $ . m is the slope of the line. The slope of the line is $ 5 $ .
We have to find the x-intercept, and y-intercept of the line $ 3x-8y-7=0 $ .
Converting into the form of $ \dfrac{x}{p}+\dfrac{y}{q}=1 $ , we get
 $ \begin{align}
  & 3x-8y=7 \\
 & \Rightarrow \dfrac{x}{{}^{7}/{}_{3}}+\dfrac{y}{{}^{-7}/{}_{8}}=1 \\
\end{align} $
Therefore, the x intercept, and y intercept of the line $ 3x-8y-7=0 $ is $ \dfrac{7}{3} $ and $ \dfrac{7}{8} $ respectively. The axes intersecting points are $ \left( \dfrac{7}{3},0 \right),\left( 0,-\dfrac{7}{8} \right) $ .
Now we place the given points and try to find their signs. If they match then they are on the same side and on the opposite sides if they don’t match.
Placing $ \left( 0,-1 \right) $ and $ \left( 0,0 \right) $ on $ 3x-8y-7 $ , we get
 $ 3\times 0-8\times 0-7=-7<0 $ and $ 3\times 0-8\times \left( -1 \right)-7=1>0 $ .
They are on the opposite sides of the line $ 3x-8y-7 $ .

Placing $ \left( 4,-3 \right) $ and $ \left( 0,1 \right) $ on $ 3x-8y-7 $ , we get
 $ 3\times 4-8\times \left( -3 \right)-7=29>0 $ and $ 3\times 0-8\times 1-7=-15<0 $ .
They are on the opposite sides of the line $ 3x-8y-7 $ .

Placing $ \left( -3,-4 \right) $ and $ \left( 1,2 \right) $ on $ 3x-8y-7 $ , we get
 $ 3\times \left( -3 \right)-8\times \left( -4 \right)-7=16>0 $ and $ 3\times 1-8\times 2-7=-20<0 $ .
They are on the opposite sides of the line $ 3x-8y-7 $ .

Placing $ \left( -1,-1 \right) $ and $ \left( 3,7 \right) $ on $ 3x-8y-7 $ , we get
\[3\times \left( -1 \right)-8\times \left( -1 \right)-7=-2<0\] and $ 3\times 3-8\times 7-7=-60<0 $ .
They are on the same side of the line $ 3x-8y-7 $ .

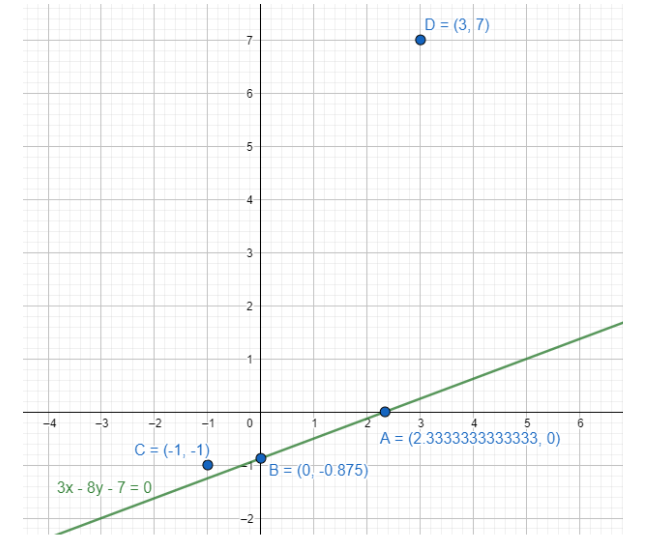
So, the correct answer is “Option D”.

Note: A line parallel to the X-axis does not intersect the X-axis at any finite distance. Hence, we cannot get any finite x-intercept of such a line. Same goes for lines parallel to the Y-axis. In case of slope of a line the range of the slope is 0 to $ \infty $ .