Question

Which of the following is/are correct

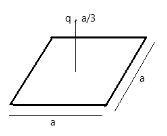
(A) Flux associated with the square plate is equal to $ \dfrac{q}{{6{\varepsilon _0}}} $
(B) Flux associated with the square plate is more than $ \dfrac{q}{{6{\varepsilon _0}}} $
(C) Flux associated with the square plate is less than $ \dfrac{q}{{6{\varepsilon _0}}} $
(D) None of the above

Answer 1

Hint : create a cubic Gaussian surface with sides equal to the side of the square plate. The total electric flux through a closed surface is independent of the size of the surface. Flux, in general, is equal to the electric field multiplied by the area of a surface.

Formula used: In this solution we will be using the following formula;
 $ \phi = EA $ where $ \phi $ is the electric flux through a surface of area $ A $ , and $ E $ is the electric field at the surface.
 $ EA = \dfrac{q}{{{\varepsilon _0}}} $ where $ q $ is the enclosed charge, and $ {\varepsilon _0} $ is the permittivity of free space.

Complete step by step answer
To know the flux through the square plate, let’s assume a cubic Gaussian surface enclosing a charge $ q $ . Now, according to gauss’s law which in statement says that the total electric flux through a surface enclosing a charge proportional to the charge enclosed irrespective of the total area of the surface. Mathematically stated in its constant form as $ EA = \dfrac{q}{{{\varepsilon _0}}} $ , where $ q $ is the enclosed charge, and $ {\varepsilon _0} $ is the permittivity of free space, and $ A $ must be a closed surface.
Hence, for our Gaussian surface, the total flux through the entire cube is
 $ \phi = \dfrac{q}{{{\varepsilon _0}}} $ . If the charge is lies exactly at the centre of the box i.e. at $ \dfrac{a}{2} $ distance away, then the flux through one of its sides is
 $ \phi = \dfrac{q}{{6{\varepsilon _0}}} $ , since a cube has six sides.
Now since, $ \phi = EA $ and $ E $ is inversely proportional to the square of the distance, then at $ \dfrac{a}{3} $ $ \left( {\dfrac{a}{3} < \dfrac{a}{2}} \right) $ distance away $ {E_{\dfrac{a}{3}}} > {E_{\dfrac{a}{2}}} $ . Hence
 $ {\phi _{\dfrac{a}{3}}} > {\phi _{\dfrac{a}{2}}} $
Hence, $ {\phi _{\dfrac{a}{3}}} > \dfrac{q}{{6{\varepsilon _0}}} $
Thus, the correct option is B.

Note
For clarity, the flux for distance $ \dfrac{a}{3} $ is greater than for distance $ \dfrac{a}{2} $ because the surface area $ A $ of the plate is constant in both cases. However, for closed surfaces the total flux is dependent of the location of the charge (as long as it is within the surface) is because when you move closer to one surface if the cube, you move farther from another surface by the same amount, thus the increase in flux for the closer surface perfectly balances the decrease for the farther surface and thus the total becomes constant.