Question

Which of the following does not have a magnetic moment of \[1.73\,B.M.\] ?
A. \[O_2^ + \]
B. \[O_2^ - \]
C. \[\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]C{l_2}\]
D. \[CuI\]

Answer 1

Hint: Magnetic moment is $\mu$, where n is the no. of unpaired electrons of the compound. Calculate the value of n by equating the magnetic moment formula. then count the number of unpaired electrons that are present in each of the suggested choices. The molecule will have a magnetic moment of \[1.73\,B.M.\] if the number of unpaired electrons in it matches the number n.

Formula used:
The following is the formula for calculating magnetic moment:
\[\mu = \sqrt {n\left( {n + 2} \right)} \]
Here, \[\mu \] is magnetic moment, and \[n\] is the number of unpaired electrons.

Complete Step by Step Answer:
Let’s calculate the number of unpaired electrons for magnetic moment \[1.73\,B.M.\] as follows:
\[ \mu = \sqrt {n\left( {n + 2} \right)} \\
   \Rightarrow 1.73 = \sqrt {n\left( {n + 2} \right)} \\
   \Rightarrow n\left( {n + 2} \right) = {\left( {1.73} \right)^2} \\ \]
Further solving,
 \[ {n^2} + 2n = 3 \\
   \Rightarrow {n^2} + 2n - 3 = 0 \\
   \Rightarrow {n^2} + 3n - n - 3 = 0 \\ \]
\[ \Rightarrow n\left( {n + 3} \right) - 1\left( {n + 3} \right) = 0 \\
   \Rightarrow \left( {n + 3} \right)\left( {n - 1} \right) = 0 \\
   \Rightarrow n = - 3\,or\,n = 1 \\ \]

The no. of unpaired electrons cannot be negative. Therefore, the value of n is 1.
So, we can say that any species having one unpaired electron will have a magnetic moment of \[1.73\,B.M.\]
The electronic configuration of \[O_2^ + \] is as follows:
\[\sigma 1{s^2} < {\sigma ^*}1{s^2} < \sigma 2{s^2} < {\sigma ^*}2{s^2} < \sigma 2p_z^2 < \pi 2p_x^2 = \pi 2p_y^2 < \pi 2p_x^1 = \pi 2p_y^0\]
From the electronic configuration, there is one unpaired electron in \[O_2^ + \].
Therefore, the magnetic moment of \[O_2^ + \] is \[1.73\,B.M.\] .
The electronic configuration of \[O_2^ - \] is as follows:
\[\sigma 1{s^2} < {\sigma ^*}1{s^2} < \sigma 2{s^2} < {\sigma ^*}2{s^2} < \sigma 2p_z^2 < \pi 2p_x^2 = \pi 2p_y^2 < \pi 2p_x^2 = \pi 2p_y^1\]
From the electronic configuration, there is one unpaired electron in \[O_2^ - \].
Therefore, the magnetic moment of \[O_2^ - \] is \[1.73\,B.M.\] .

Electronic configuration of \[Cu\] is as follows:
\[Cu:\left[ {Ar} \right]3{d^{10}}4{s^1}\]
In \[\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]C{l_2}\] , copper is in \[C{u^{2 + }}\] oxidation state.
Electronic configuration of \[C{u^{2 + }}\] is as follows:
\[C{u^{2 + }}:\left[ {Ar} \right]3{d^9}4{s^0}\]

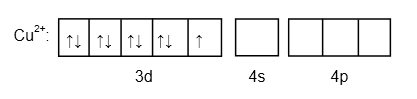
Image: Outermost electronic configuration of \[C{u^{2 + }}\]
There is one unpaired electron in \[\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]C{l_2}\] .
Therefore, the magnetic moment of \[\left[ {Cu{{\left( {N{H_3}} \right)}_4}} \right]C{l_2}\] is \[1.73\,B.M.\] .

In \[CuI\] , copper is in \[C{u^ + }\] oxidation state.
Electronic configuration of \[C{u^ + }\] is as follows:
\[C{u^ + }:\left[ {Ar} \right]3{d^{10}}4{s^0}\]

Image: Outermost electronic configuration of \[C{u^ + }\]
There is no unpaired in \[C{u^ + }\] .
The magnetic moment for zero unpaired electron species is zero.

Therefore, the correct answer is option D. \[CuI\] .

Note: A magnetic dipole is a physical thing, whereas a magnetic moment is a numerical measure of the strength of a dipole. Magnetic moment should never be confused with a magnetic dipole.