Question

Which of the following arrangements, A or B has the lower Combined resistance?

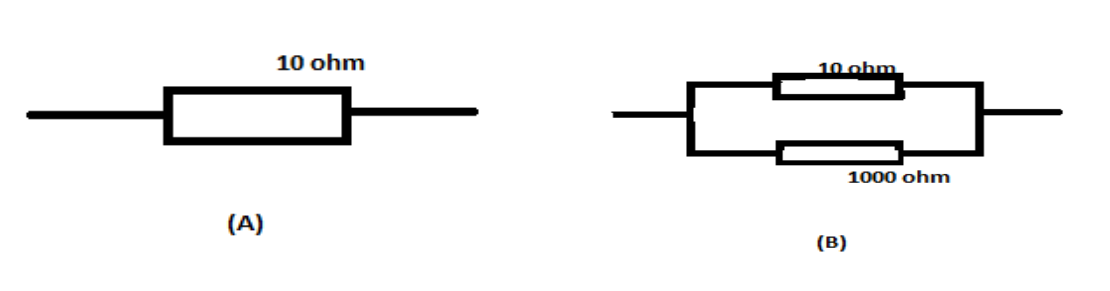
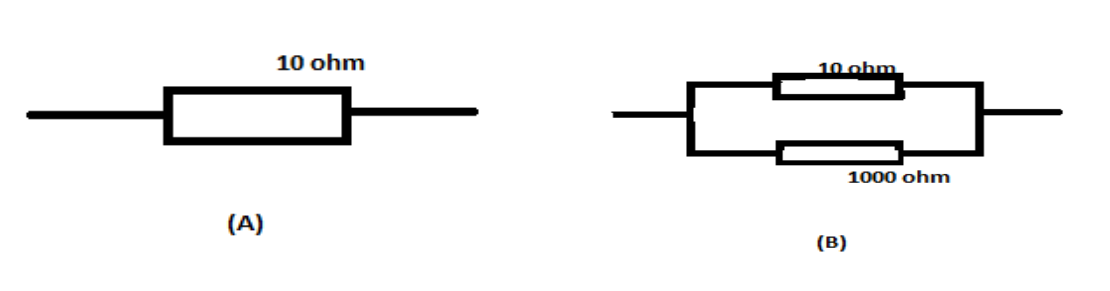
Answer 1

Hint: Resistance B is arranged in Parallel, so we have to find the total resistance value to find the lower combined resistance.
In the parallel resistance, the sum of the current through each path is equal to the total current that flows from the source.
In a parallel circuit, the total resistance value decreases when we add more components.

Formula used:
The total resistance of “B” can be calculated by using the following formula,
$\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$
In the above equation, ${R_1}$ is $10\Omega $ and the resistance ${R_2}$ is $1000\Omega $ .

Complete step by step solution:
The combined resistance of an arrangement Scan be calculated as follows, by substituting the resistance R1 and R2 in the above equation
\[{R_1} = 10\Omega \] and ${R_2} = 1000\Omega $,
\[\dfrac{1}{R} = \dfrac{1}{{10}} + \dfrac{1}{{1000}}\]
By simplifying the above equation,
\[\dfrac{1}{R} = \dfrac{{(100 + 1)}}{{1000}}\]
Then the \[R\] Will be,
\[R = \dfrac{{1000}}{{101}}\]
After the simplification, the combined resistance will be,
\[R = 9.9\Omega \]
Let’s Compare the resistance “A” and “B”
A= $10\Omega $ and B= $9.9\Omega $
$10\Omega $ $ \geqslant $ $9.9\Omega $
Therefore, the arrangement “B” has a lower combined resistance.

Note:
The combined resistor in parallel is lower than the lower resistance of individual resistors.
In a parallel circuit, the potential difference is the same, but the current gets varied, which is dependent on individual resistance.