Question

Which of the following are alicyclic compounds?
a.) Cyclopropane
b.) Ethane
c.) Benzene
d.) Pyridine

Answer 1

Hint: To answer this question, we must know what alicyclic compounds are. An alicyclic compound is both an aliphatic and a cyclic organic compound. These contain one or more all-carbon rings that can be either saturated or unsaturated, but lack an aromatic character. An alicyclic compound could have attached one or more aliphatic side chains.

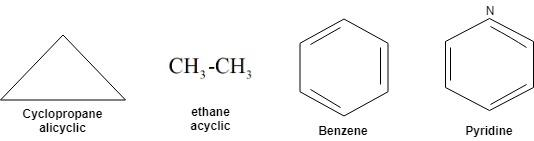
Complete answer:
From the above figure we can conclude that option A i.e. Cyclopropane is the right answer.
Cyclopropane, also known as trim ethylene, toxic, colorless gas which has been used as a general anesthetic in medicine since 1934. Cyclopropane does not irritate mucous membranes and does not inhibit breathing. Rapid and smooth induction and emergence from cyclopropane anesthesia is typically. Inhalation is used to deliver a mixture of around 5 to 20 per cent cyclopropane in oxygen. It is typically used in a closed (rebreathing) system because of the flammability and cost of cyclopropane, in which an absorbent chemical such as soda lime absorbs exhaled carbon dioxide and the anesthetic is recirculated. The molecular formula for this is $$C_3{H}_6$$.


Note: Alicyclic compound is a broad class of organic compounds in which three or more carbon atoms are bound together in a ring. The bonds between pairs of adjacent atoms may all be of the type designated single bonds (including two electrons), or some of them may be double or triple bonds (with four or six electrons, respectively); six-membered rings for which a system of single and double alternating bonds may be envisaged, but belong to another important class (aromatic compounds), distinguished from the a alicyclic. Those alicyclic compounds in which the ring contains three or four carbon atoms are less stable than those with larger rings, because the angles formed by adjacent covalent bonds are smaller than is required for maximum efficiency. All the bond angles in the larger rings have the desired value (around 109.5 °) thus, the atoms in the ring do not lie in one plane. Similar angle restrictions in double and triple bonds affect the stability of an alicyclic compound which contain these bonds.