Question

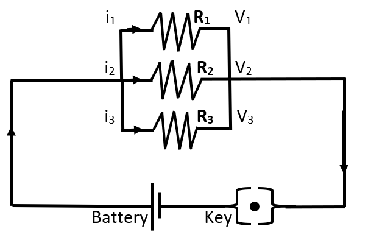
Which is the correct answer for the circuit given below:

$\begin{align}
  & (A){{i}_{1}}={{i}_{2}}={{i}_{3}} \\
 & (B){{V}_{1}}={{V}_{2}}={{V}_{3}} \\
 & (C){{R}_{1}}={{R}_{2}}={{R}_{3}} \\
 & (D)\dfrac{{{V}_{1}}}{{{R}_{1}}}=\dfrac{{{V}_{2}}}{{{R}_{2}}}=\dfrac{{{V}_{3}}}{{{R}_{3}}} \\
\end{align}$

Answer 1

Hint: In the given circuit diagram, the resistances are connected in parallel. And the given current is through each resistance in separate branches. Also, the potential differences are to be considered across the three resistances. We shall use these conditions to comment on the following options whether being true or false.

Complete step-by-step solution:
In the above circuital diagram, we can clearly see that all the resistances are connected in parallel with each other. This means that the potential difference across their terminal is equal. Hence, we can say that:
$\Rightarrow {{V}_{1}}={{V}_{2}}={{V}_{3}}$
Now, for the resistances, they are the property of a substance. And nothing has been mentioned about them in the question. So, we cannot say, if they are equal or unequal, small or high, anything. Any statement on them is ambiguous. Thus,
 $\Rightarrow {{R}_{1}}={{R}_{2}}={{R}_{3}}$ is a false statement.
Now, the current in each branch is also related to the resistance as current in a branch is inversely proportional to the resistance in that branch. Hence, we cannot say anything about current too, that means:
$\Rightarrow {{i}_{1}}={{i}_{2}}={{i}_{3}}$ is also a false statement.
Now, these currents can be written as:
$\begin{align}
  & \Rightarrow {{i}_{1}}=\dfrac{{{V}_{1}}}{{{R}_{1}}} \\
 & \Rightarrow {{i}_{2}}=\dfrac{{{V}_{2}}}{{{R}_{2}}} \\
 & \Rightarrow {{i}_{3}}=\dfrac{{{V}_{3}}}{{{R}_{3}}} \\
\end{align}$
Thus, the fourth option is the same as the first option. That is we cannot comment on it. Hence,
$\Rightarrow \dfrac{{{V}_{1}}}{{{R}_{1}}}=\dfrac{{{V}_{2}}}{{{R}_{2}}}=\dfrac{{{V}_{3}}}{{{R}_{3}}}$ is also a false statement.
Thus, from our above analysis of the given circuit diagram, only ${{V}_{1}}={{V}_{2}}={{V}_{3}}$ is the correct statement.
Hence, option (B) is the only correct option.

Note: If in our above circuit, any relation would have been given between the currents in the branches or the three resistances, we would have been able to conclude a statement on how they are related to each other in magnitude. But, since nothing has been mentioned, it is totally absurd and meaningless to comment on them.