Question

What is the square root of $146$ ?

Answer 1

Hint: We first perform the prime factorisation of $146$ . Upon prime factorisation, we see that $146$ consists of only two prime numbers; $2,73$ , and that too only once. So, the square root of $146$ becomes $\sqrt{2}\times \sqrt{73}$ . We have to now use a calculator to find the respective root values, giving the answer as $12.083$ .

Complete step-by-step solution:
Indices are a representation of repetitive multiplication of the same kind. Repetitive multiplication if shown in the form $a\times a\times a\times a\times ....$ will become tedious and time taking. So, in order to avoid it, we have implemented the indices representation. Here, we represent the original number with the number of multiplications written as a superscript. For example, three times multiplication of two will be $2\times 2\times 2$ which can be written as ${{2}^{3}}$ . Indices can be called as an operation of numbers. The inverse operation of indices is called square rooting, cube rooting and so on. Square rooting means to break down a number into two other similar numbers such that their product gives the original number. For example, the square root of $4$ gives $2$ since $2\times 2$ implies $4$ .
In square rooting, we use prime factorisation to break down a number into its prime factors. Prime factorisation gives the product of prime factors. For example, the prime factorisation of $146$ gives,
\[\begin{align}
  & 2\left| \!{\underline {\,
  146 \,}} \right. \\
 & \left| \!{\underline {\,
  73 \,}} \right. \\
\end{align}\]
Which can be written as $2\times 73$ . After square rooting, clearly it gives $\sqrt{2}\times \sqrt{73}$ . But it can be written in decimals as $1.414\times 8.544=12.083$ .
Therefore, we can conclude that the square root of $146$ is $12.083$ .

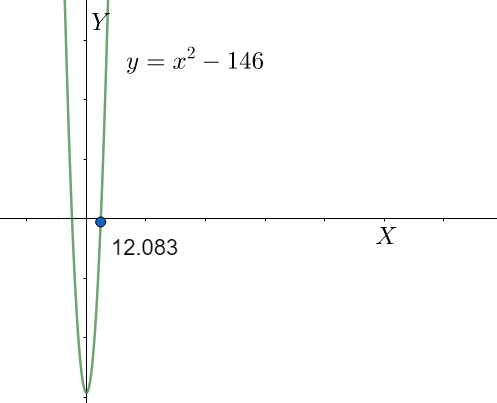
Note: The square root of $146$ can also be found out using the graphical method. We draw the graph of $y={{x}^{2}}-146$ and then find the values of x where the function becomes zero. We take only the positive root which is $12.083$ .