Question

What is the domain of \[y=\sqrt{4-{{x}^{2}}}\]?

Answer 1

Hint: In this problem, we have to find the domain of the given function \[y=\sqrt{4-{{x}^{2}}}\]. Here we can first find the x-intercept and the y-intercept, we can then plot them in the graph to find where the function is defined. We can then write the domain of the given function.

Complete step-by-step solution:
Here we have to find the domain of the given function \[y=\sqrt{4-{{x}^{2}}}\].
We can now find the x-intercept and the y-intercept for the given function.
We know that at x-intercept the value of y is 0 and at y-intercept the value of x is 0. By using this, we can find the intercepts value.
We can now find the point at x, where y is 0.
\[\begin{align}
  & \Rightarrow 0=4-{{x}^{2}}=\left( 2+x \right)\left( 2-x \right) \\
 & \Rightarrow x=\pm 2 \\
\end{align}\]
The x-intercept is at \[\left( 2,0 \right),\left( -2,0 \right)\].
We can now find the y-intercept, where x is 0.
\[\Rightarrow y=\sqrt{4-0}=2\]
 The y-intercept is at \[\left( 0,2 \right)\].
We can now plot the points in the graph for the given semicircle equation.

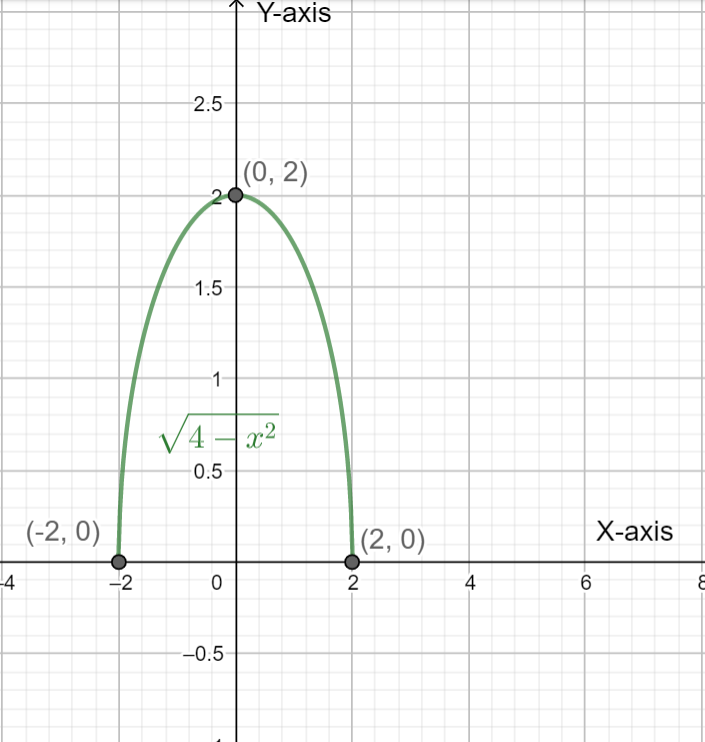
We can now see that the domain is \[-2\le x\le 2\].
Therefore, the required domain is \[\left[ -2,2 \right]\].

Note: We should always remember that at x-intercept the value of y is 0 and at y-intercept the value of x is 0. We should know that the domain of the function is the set of all possible values which qualify as input to a function or we can say it as the entire set of values possible for independent variables.