Question

What is $P\left( 0.59 < z < 1.77 \right)?$

Answer 1

Hint: We need to use the concept of normal distribution of standard deviation in order to solve this question. For the question, we need to calculate the area under the normal distribution curve for the given z values. This can be done by referring the table for z values for 1.77 and 0.59 and subtracting the two to get the area under the curve.

Complete step by step solution:
In order to answer this question, let us describe the meaning of the standard normal distribution curve. It is the probability distribution for a random variable with mean as 0 and standard deviation as 1. The curve for the given question along with the bounded values are shown in the figure.

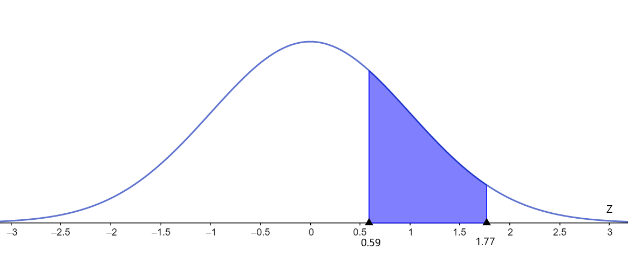
The values of z lie in the interval 0.59 and 1.77. We are required to calculate the area under the curve. This can be done by referring to the normal distribution table given below.

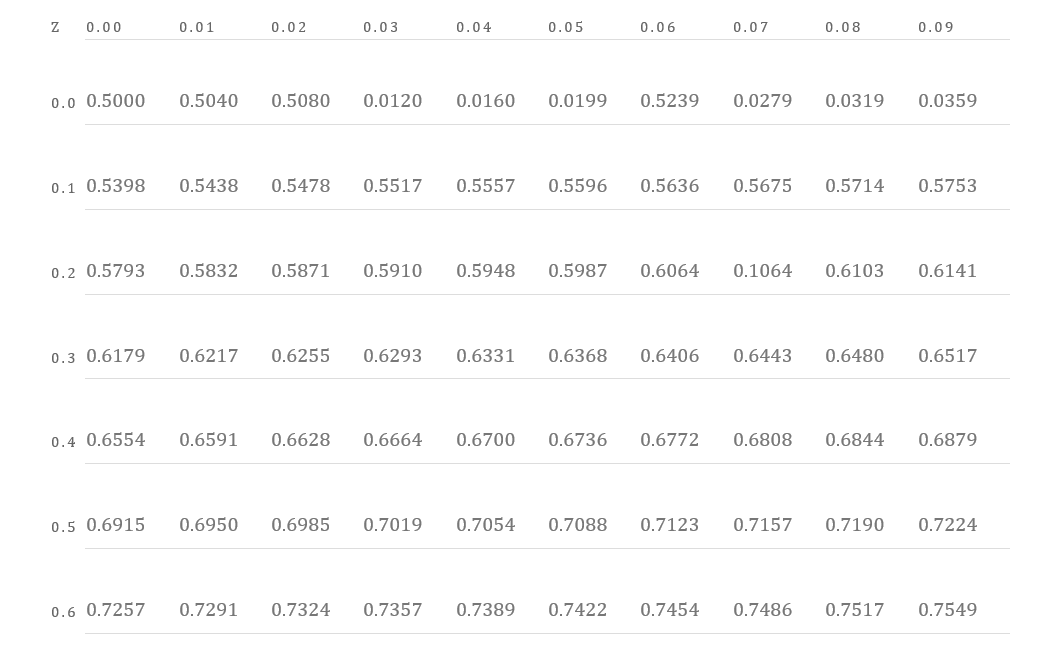
Looking at the table above, corresponding to the z value, we need to calculate the probability value. Consider the lower limit of 0.59. Looking at the table for a value with 0.5 in the left most column. Then we move along that row under the column 0.09 and obtain the value 0.7224. Next we need to calculate the probability value for the z value 1.77.

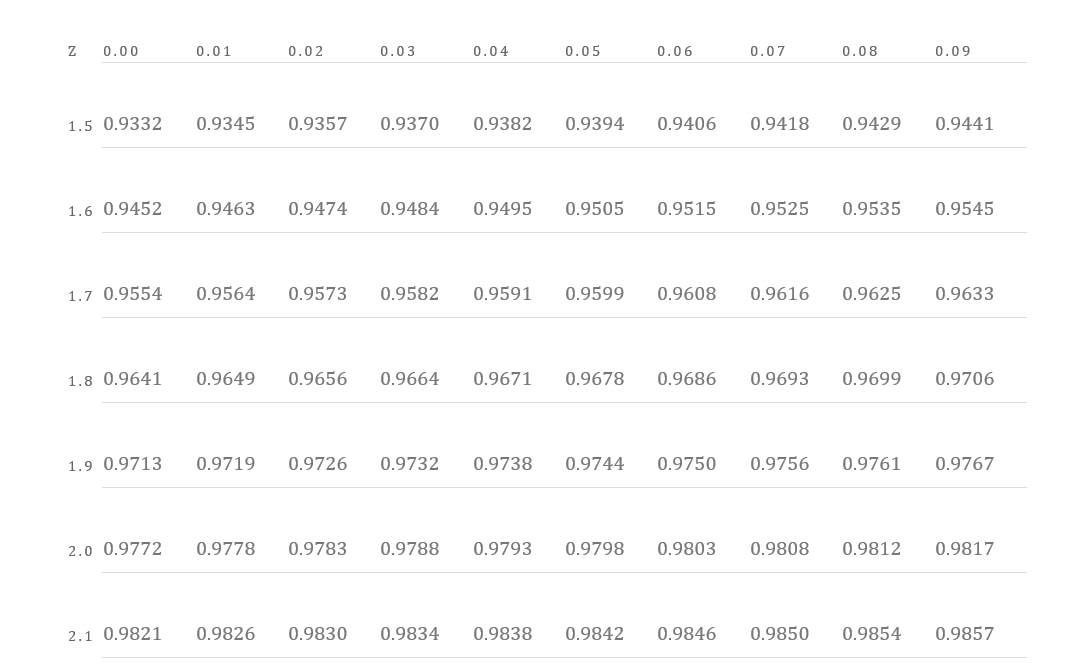
Looking at the table above, corresponding to the z value 1.77, we need to calculate the probability value. Looking at the table for a value with 1.7 in the left most column. Then we move along that row under the column 0.07 and obtain the value 0.9616.
We now subtract the two probability values to obtain the answer.
$\Rightarrow P\left( 0.59 < z < 1.77 \right)=0.9616-0.7224$
Subtracting the two values,
$\Rightarrow P\left( 0.59 < z < 1.77 \right)=0.2392$
Hence, the answer obtained is 0.2392.

Note: We need to know the concept of normal distribution in order to solve many probabilistic sums. Care must be taken while reading the values from the tables because students tend to make an error in this step while observing. One wrong reading could lead to a completely wrong answer.