Question

What is Demorgan's first law?

Answer 1

Hint: De Morgan theorem consists of two theorems. Equation of the 1st theorem is $\overline{A+B}=\overline{A}.\overline{B}$ and equation of 2nd theorem is\[\overline{A.B}=\overline{A}+\overline{B}\]. To prove the equation of statement, put value zero in place of A and B. Use operation and value from the truth table of OR & AND gate. You will see that the left hand side will be equal to the right hand side.

Complete step-by-step answer:
In algebra, De Morgan's First law or First Condition states that the complement of the product of two variables is corresponding to the sum of the complement of each variable. In other words, according to De Morgan's first laws or first theorem if 'A' and 'B'are the two variables or Boolean numbers. This indicates that the NAND gate function is similar to OR gate function with complemented inputs. Then accordingly the equations are as below;

For Nor GATE
\[ Y =\overline{A}+\overline{B}\]

For the bubbled AND Gate
$Y = \overline{A}.\overline{B}$

Symbolic representation of De Morgan's First Law Theorem Since the NOR and the bubbled gates can be interchanged, i.e., both gates have just similar outputs for the identical set of inputs.
Hence, the equation can be algebraically represented in the figure shown below.
This equation presented above is known as DeMorgan's First Theorem. The symbolic illustration of the theorem is presented as shown below.

Role of Complementation:- Bars Complementation bars are proposed to operate as grouping symbols. Hence, when a bar is broken, the expressions beneath it should remain grouped. Parentheses may be positioned around these grouped expressions as an assistance to give a miss to changing precedence.

Verifying De Morgan's First Theorem Using Truth Table :-
According to De Morgan's First law, it proves that in conditions where two (or more) input variables are Added and negated, they are equal to the OR of the complements of the separate variables. Hence, the equivalent of the NAND function and is a negative-OR function verifying that A.B = A+B and we can literally prove this using the following table.

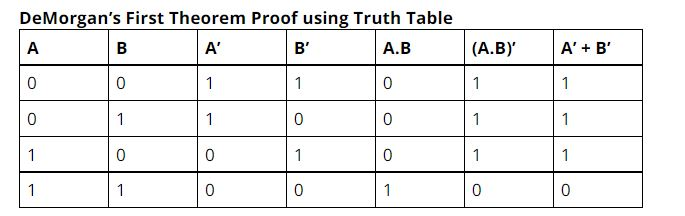
Now that you have already understood De Morgan's First Theorem using the Truth
Table. We will make you familiar with another way to prove the theorem i.e. by using logic gates.
This is to say, we can also prove that A.B = A+B using logic gates as hereinafter.

Note: In this theorem ‘+’ represent OR operation and ‘.’ represent AND operation. This theorem can be proved in different ways. In this theorem we put 0 value in the theorem equation. You can put 1 value instead of 0 value. You will get the same result and from this also we can prove de Morgan’s theorem.