Question

Weights of 20 kg and 30 kg are suspended from the ends of a light rod 5m long. At which point the rod must be suspended by means of a string to keep it horizontal?
(a) At 3m from 30kg weight
(b) At 4m from 20kg weight
(c) At 3m from 20kg weight
(d) At 4m from 30kg weight

Answer 1

Hint: When the same mass is attached to a rod, the torque will act due to that mass which is given as the product of the force due to that mass and distance from that mass from the point of suspension. When the same other mass is attached to the other end, this torque will be balanced by suspending the rod at a point of the centre of gravity.

Complete step by step answer:
Let us assume the rod is suspended at a point P which is x m from the end where 20kg of mass is attached as shown in the below figure.

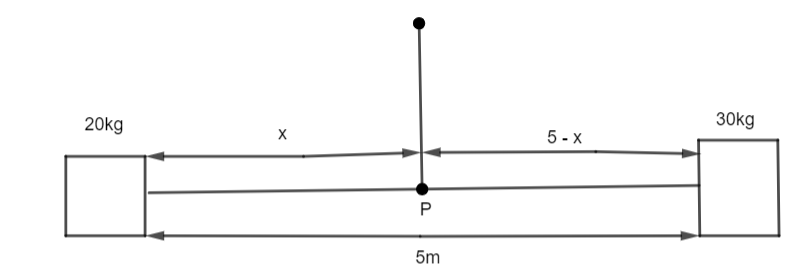
Since the rod is 5m long, the distance of the point from the other end where 30kg of the mass is attached will be 5 – x. When we suspend a rod and attach the weights on both the ends, a torque will act on the rod due to the weights. This torque (nothing but the moment of force) is given by the product of force and the distance from the centre of gravity.
So, here point P is the centre of gravity of a given system and force is the gravitational force, i.e. their weights.
\[\text{Torque due to 20kg of mass}=20\times g\times x\]
\[\text{Torque due to 30kg of mass}=30\times g\times \left( 5-x \right)\]
where g is the acceleration due to gravity.
We have,
Torque due to 20kg of mass = Torque due to 30kg of mass
Therefore,
\[20\times g\times x=30\times g\times \left( 5-x \right)\]
\[\Rightarrow 20x=150-30x\]
\[\Rightarrow 20x+30x=150\]
\[\Rightarrow 50x=150\]
\[\Rightarrow x=\dfrac{150}{50}\]
\[\Rightarrow x=3m\]
Hence, the rod must be suspended at the distance of 3m from the end where 20kg of mass is attached. Or in other words, the rod must be suspended at the distance (5 – 3 = 2m) from the end where 30 kg of mass is attached.
Hence, the option (c) is the right answer.

Note:
On the same kind of principle, a balance is designed where it is suspended at the centre and the pans are suspended by an equal length of the strings. So in order to have the same moment of force or the torque, mass added must be the same. Also, note that the point of suspension will be close to the end where more mass is attached.