Question

We wish to obtain a capacitance of \[5\mu F\], by using some capacitors, each of \[2\,\mu F\] . Then the minimum number of capacitors required is?
A. 3
B. 4
C. 5
D. not possible

Answer 1

Hint: We know that capacitors work in an opposite way as compared to resistors when connected in either series or parallel combination. So, we will start by checking the equivalent capacitance of capacitors connected in series and in parallel. We see both conditions do not give equivalent capacitance of \[5\mu F\]. Hence we will combine capacitors in parallel and series and look at the minimum number of capacitors required.

Complete step by step answer:
As mentioned in the hint above the capacitors in series connection is given by :
\[C_{(eq)} = C_1 + C_2 + ...... + C_n\].............(in parallel)
And ; \[\dfrac{1}{{C(eq)}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + ...... + \dfrac{1}{{C_3}}\]......(in series)
The case of series combination we see that: \[\dfrac{1}{{C(eq)}} = \dfrac{1}{2} + \dfrac{1}{2}\]
\[\dfrac{1}{{C(eq)}} = \dfrac{1}{1} = 1\mu F\]
And in case or parallel: \[C_{(eq)} = 2 + 2 = 4\mu F\]
But we need \[5\mu F\], hence we will try making different combinations. This can be achieved by adding 2 capacitors in series, it will give effective capacitance of \[1\mu F\].Now if we add 2 capacitors in parallel to the earlier circuit we get effective capacitance as \[5\mu F\].

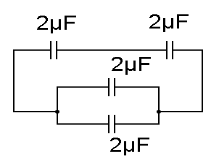
C(eq) because the series is 1microfarad and because of the parallel connection is 4 microfarad. Hence the effective capacitance of circuit \[ = 1\mu F + 4\mu F\].
\[C_{(eq)} = 5\mu F\]
Hence looking at all the observations above we see that to make capacitance of \[5\mu F\] using capacitors of \[2\mu F\], minimum 4 capacitors will be required.

Hence the correct option is B.

Note: We should remember that capacitors in series is given by \[\dfrac{1}{{C(eq)}} = \dfrac{1}{{C_1}} + \dfrac{1}{{C_2}} + ...... + \dfrac{1}{{C_3}}\] and the capacitor in parallel is given by \[C(eq) = C_1 + C_2 + ...... + C_n\]. It should not be confused with a combination of resistors.Here C(eq) is equivalent capacitance. There can be many other combinations but keep in mind we need a minimum number of capacitors.