Question

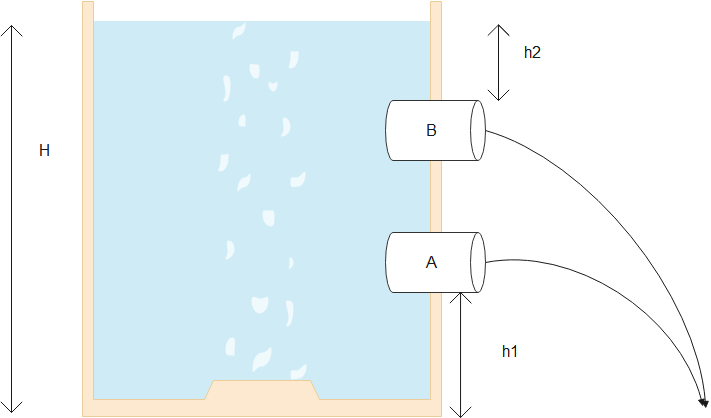
Water stands at a height H in a tall cylinder (see figure). Two holes A and B are made on the sides of the cylinder. If hole A is at a height ${{h}_{1}}$above the ground, what is the height of hole B above the ground so that the two streams of water emerging from holes A and B strikes the ground at the same point?

Answer 1

>Hint: In this question we are asked about the height of the hole B from the ground and we are given the condition that the waterfalls at the same point on the ground from both the holes, this means that we are given that the range of the water stream from both the point is same. In this case we can equate the range of hole A and Hole B.

Step by Step solution:
First, we need to write about all the given quantities.
We are given that H is the height of water from the ground and ${{h}_{1}}$ is the height to hole A from the ground and we can assume that ${{h}_{2}}$ is the depth of hole B from the water level.

According to the given condition we can assume that Range for both the holes are equal
This means ${{R}_{1}}={{R}_{2}}=R$

We know that range is equal to $R=ut$
So ${{u}_{1}}{{t}_{1}}={{u}_{2}}{{t}_{2}}$

Where ${{u}_{1}}$ is velocity of efflux at hole A and ${{u}_{2}}$ is the velocity of efflux at hole B
${{u}_{1}}=\sqrt{2g(H-{{h}_{1}})}$ and ${{u}_{2}}=\sqrt{2g{{h}_{2}}}$
And ${{t}_{1}}$ is the time taken by water stream to reach ground from hole A
And ${{t}_{2}}$ is the time taken by water stream to reach ground from hole B
Where ${{t}_{1}}$ =$\sqrt{\dfrac{2(H-{{h}_{1}})}{g}}$ and ${{t}_{2}}$= $\sqrt{\dfrac{2{{h}_{2}}}{g}}$

Put these values in equation ${{u}_{1}}{{t}_{1}}={{u}_{2}}{{t}_{2}}$
We get \[\sqrt{2g(H-{{h}_{1}})}\times \sqrt{\dfrac{2(H-{{h}_{1}})}{g}}=\sqrt{2g{{h}_{2}}}\times \sqrt{\dfrac{2{{h}_{2}}}{g}}\]

On solving this we get $H-{{h}_{2}}=\sqrt{2{{h}_{1}}H}+{{h}_{1}}$

So our required answer is the height of hole B from the ground is $\sqrt{2{{h}_{1}}H}+{{h}_{1}}$.

Note:
Since we are not given with any numerical quantity hence our answer will be in terms of ${{h}_{1}}$and H only, but if in some question we are given with any numerical value for the height of water above the ground and the height of any one the hole from the ground the we can find the height of another hole just by putting the numerical value of H and ${{h}_{1}}$.