Question

Vibration of magnetometer works on the principle of
A. Torque acting on bar magnet and rotational inertia
B. Force acting on bar magnet and rotational inertia.
C. both force and torque acting on magnet
D. Neither force nor torque.

Answer 1

Hint: Vibration magnetometer is an instrument used to compare the magnetic moments of two magnets or to determine the horizontal component of the Earth’s magnetic field. When a magnet suspended in a uniform magnetic field (like the one due to earth’s) is displaced from its equilibrium position and it begins to vibrate simply harmonically about the direction of the field.
Formula used:
The time period of vibration magnetometer is given by
\[T=2\pi \sqrt{\dfrac{I}{m{{B}_{H}}}}\], where
$\begin{align}
  & m=\text{ magnetic moment of the magnet taken} \\
 & {{B}_{H}}=\text{ the horizontal component of earth }\!\!'\!\!\text{ s magnetic field} \\
 & I=\text{ the moment of inertia of the magnet about an axis of rotation about its center of mass} \\
 & I=\text{Mass of the magnet}\times \dfrac{{{l}^{2}}+{{b}^{2}}}{12} \\
 & l\text{ and }b\text{ are the length and bredth of the magnet} \\
\end{align}$

Complete answer:
When a bar magnet is placed in an uniform magnetic field then it will experience a force in the direction of the field due to which the bar magnet will rotate and will try to align with the magnetic field.
The magnet will experience a torque which will rotate the magnet and will try to align with the field due to the rotational inertia the bar magnet will execute simple harmonic motion.
i.e. A vibration magnetometer works on the principle of torque acting on bar magnet and rotational inertia.

So, the correct answer is “Option A”.

Additional Information:

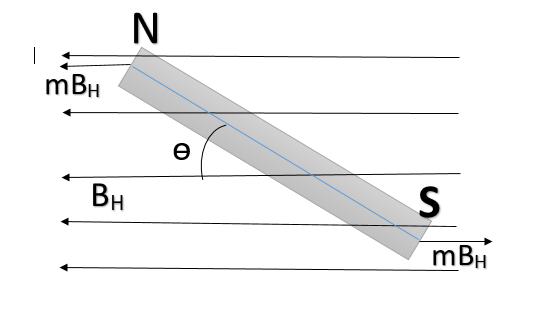
Torque acting on the dipole will be $\tau =m{{B}_{H}}(2l\sin \theta )=2ml{{B}_{H}}\sin \theta =M{{B}_{H}}\sin \theta $

Where
$\begin{align}
  & 2l=\text{ length of the bar magnet}\text{.} \\
 & \text{M=}2ml=\text{ magnetic dipole moment} \\
\end{align}$

For small $\theta$,$\tau =M{{B}_{H}}\theta $

If $\alpha =\text{ angular acceleration and }I=\text{ moment of inertia}$, then
${{I}_{\alpha }}=M{{B}_{H}}\theta $
So time period of oscillation is
\[T=2\pi \sqrt{\dfrac{I\theta }{{{I}_{\alpha }}}}=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\]
Calculating the horizontal component of earth’s magnetic field:
With the help of a vibration magnetometer we can measure the time period of say $T\text{ and }T'$ of vibration of the same magnet at two given places. Let ${{B}_{H}}\text{ and }{{B}_{H}}'$ are the horizontal component of earth’s magnetic field at these places. Then

\[\begin{align}
  & T=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}}\text{ and }T'=2\pi \sqrt{\dfrac{I}{M{{B}_{H}}}} \\
 & \Rightarrow \dfrac{T}{T'}=\sqrt{\dfrac{{{B}_{H}}'}{{{B}_{H}}}} \\
 & \Rightarrow \dfrac{{{B}_{H}}}{{{B}_{H}}'}=\dfrac{T{{'}^{2}}}{{{T}^{2}}} \\
\end{align}\]

Note:
Vibration magnetometer works on the principle of torque and rotation in the uniform magnetic field. If the field is non-uniform or the field is very strong the magnet will not oscillate and will stop when aligned with the field. So the vibration magnetometer only works when the field is uniform and not very strong.