Question

Verify LMVT for the function $f\left( x \right) = x + \dfrac{1}{x},x \in \left[ {1,3} \right]$

Answer 1

Hint – In order to verify LMVT for the given function, we will take help of the graph and LMVT to solve the given equation and after getting the result from LMVT we will check if it lies between the mentioned domain.

Complete step by step answer:
It is given that $f\left( x \right) = x + \dfrac{1}{x},x \in \left[ {1,3} \right]$
$ \Rightarrow \dfrac{{{x^2} + 1}}{x}$
Now, we know the graph of above equation

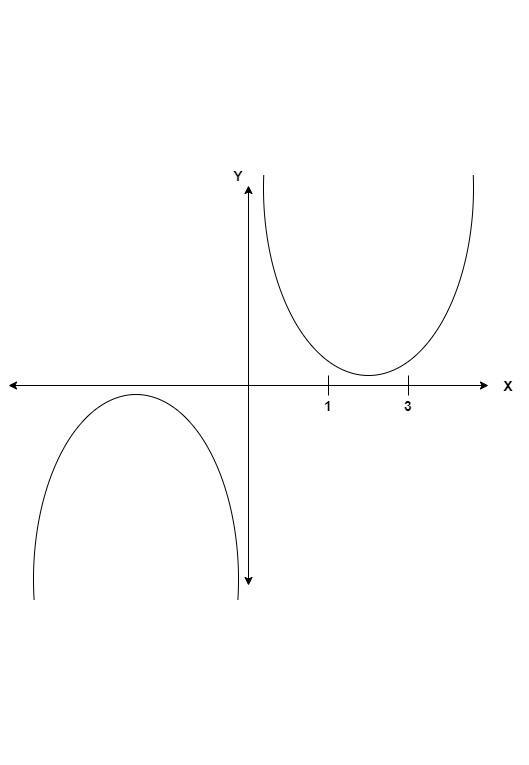
Hence, from graph we can see that
$\dfrac{{{x^2} + 1}}{x}$, $x + \dfrac{1}{x}$ are differentiable too.
So, we will differentiate it by using Lagrange’s Mean Value Theorem i.e.
Let $f:\left[ {a,b} \right] \to R$ be a continuous function, differentiable on the open interval $\left( {a,b} \right)$. Then there exists some $c \in \left( {a,b} \right)$ such that $f'\left( c \right) = \dfrac{{f\left( b \right) - f\left( a \right)}}{{b - a}}$, where $f\left( c \right) = f\left( x \right) = x + \dfrac{1}{x}$ and $\left( {a,b} \right) = \left( {1,3} \right)$ which implies that $a = 1,b = 3$.
$\therefore f'\left( x \right) = 1 - \dfrac{1}{{{x^2}}}$ and $f\left( a \right) = f\left( 1 \right) = 1 + \dfrac{1}{1} = 1 + 1 = 2$, $f\left( b \right) = f\left( 3 \right) = 3 + \dfrac{1}{3} = \dfrac{{10}}{3}$
Now, we will put these values in above formula, to get
$ \Rightarrow 1 - \dfrac{1}{{{x^2}}} = \dfrac{{\dfrac{{10}}{3} - 2}}{{3 - 1}}$
We will solve it further,
$ \Rightarrow 1 - \dfrac{1}{{{x^2}}} = \dfrac{{\dfrac{{10 - 6}}{3}}}{2} = \dfrac{4}{{3 \times 2}} = \dfrac{4}{6} = \dfrac{2}{3}$
Simplifying it further, we will get
$
   \Rightarrow 1 - \dfrac{2}{3} = \dfrac{1}{{{x^2}}} \\
   \Rightarrow \dfrac{1}{3} = \dfrac{1}{{{x^2}}} \\
 $
By cross multiplying, we get
${x^2} = 3$
Taking square both the sides,
$\therefore x = \pm \sqrt 3 $
Hence, $x = \sqrt 3 $ which lies between $\left[ {1,3} \right]$

Therefore, it satisfies LMVT.

Note – LMVT is also known as MVT “Mean Value Theorem” which states that for a given planar arc between two endpoints, there is at least one point at which the tangent to the arc is parallel to the secant through its endpoints. So, to avoid mistakes one must retain that there is only one formula for LMVT and you have to use it properly. A student should differentiate and put values carefully too