Question

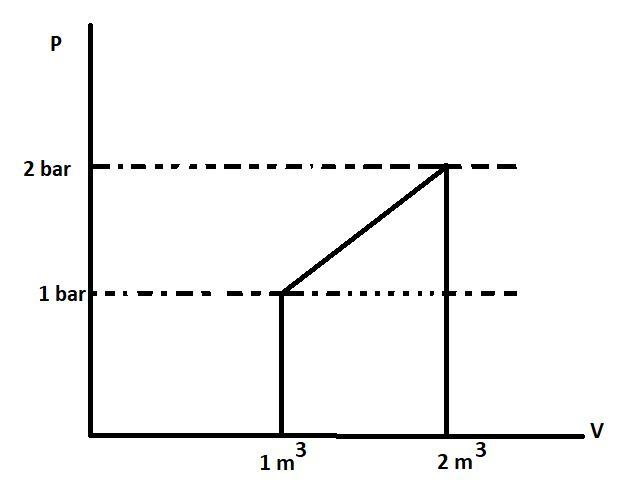
What is $\vartriangle \text{U}$ for the presence described by the figure?
Heat supplied during the process, q= 100 KJ.

A. +50 KJ
B. -50 KJ
C. -150 KJ
D. +250 KJ

Answer 1

Hint: Find the work done using the P-V graph; as the area under the P-V curve represents the work done by the gas. Then use the first law of thermodynamics to calculate $\vartriangle \text{U}$. The first law says that $\vartriangle \text{U}=\text{W+Q}$. Do convert the units into joules.

Complete answer:
Let us first find the work done by the gas using the given graph:
We know that the area under the P-V curve gives the work. This is because the formula of work done is $\text{P}\vartriangle \text{V}$. The area or work in the P-V graph is represented by :

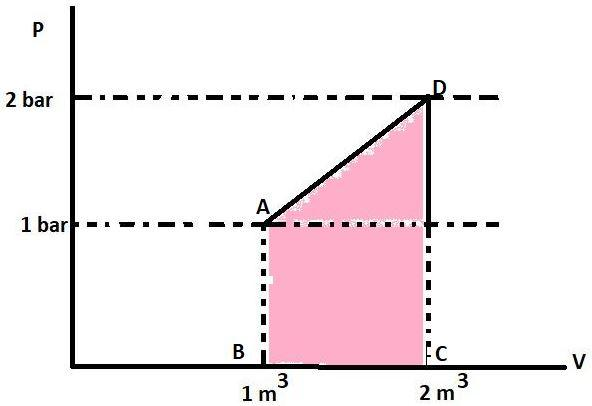
This coloured portion is a trapezium with AB and CD as its parallel sides and height between the two is $\vartriangle \text{V}$. The area of trapezium is sum of parallel sides multiplied to the height and divided by 2 or $\frac{1}{2}\times \left( \text{Sum of parallel sides} \right)\times \left( \text{Height} \right)$. The parallel sides have the value 1 bar and 2 bar respectively. The height is $\vartriangle \text{V}$ or (2-1) ${{\text{m}}^{3}}$ . So, the area will be $\frac{1}{2}\times \left( 1+2 \right)\times \left( 1 \right)$ or 1.5 bar-${{\text{m}}^{3}}$. The work in joules will be 150 KJ as $1\text{ bar-}{{\text{m}}^{3}}=100\text{ KJ}$. Work is positive because $\vartriangle \text{V}$ is positive. So, the value of W is +150 KJ.
- First law of Thermodynamics says that energy can only be converted from one form to another. It can neither be destroyed nor be created. Mathematically, its expression is $\vartriangle \text{U}=\text{W+Q}$.
Q= + 100 KJ, positive because it is added to the system from outside. Using the formula, $\vartriangle \text{U}$ will be $100+150$ or 250 KJ.
The change in internal energy or $\vartriangle \text{U}$ for the process is +250 KJ.

The correct option is ‘d’.

Note:
The unit of work done should be known which is joule. The conversion units have to be used correctly. It should be known that if $\vartriangle \text{V}$ is positive, then work will be positive and if $\vartriangle \text{V}$ is negative then, work will also be negative.