Question

\[\vartriangle ABC\] and \[\vartriangle BDE\] are two equilateral triangles such that $BD = BC$. Find the ratio of areas of aseminate \[\vartriangle ABC\] and \[\vartriangle BDE\].

Answer 1

Hint: In this question, we have the relation between the sides of two equilateral triangles. By using that we have to find the ratio of aseminate for the given equilateral triangles.
We need to first consider that the sides of an equilateral triangle are equal. Then we will calculate the area of the equilateral triangles for each case using the formula. Then we can easily find out the ratio which is required.

Formula used: The area of the equilateral triangle \[\vartriangle ABC\] is \[\dfrac{{\sqrt 3 }}{4}{a^2}\]
Where the sides of the equilateral triangle \[\vartriangle ABC\] is \[a\].

Complete step-by-step solution:
It is given that \[\vartriangle ABC\] and \[\vartriangle BDE\] are two equilateral triangles such that $BD = BC$.

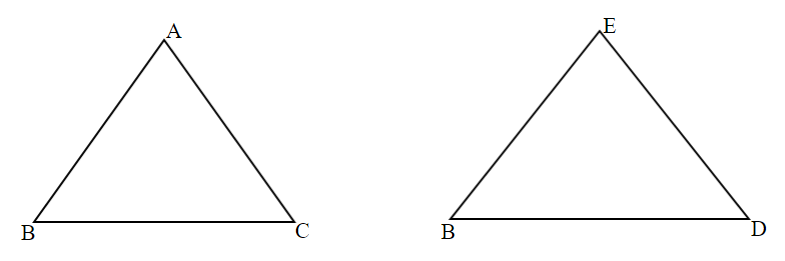
We need to find out the ratio of areas of the equilateral triangles \[\vartriangle ABC\] and \[\vartriangle BDE\].
Since \[\vartriangle ABC\] is a equilateral triangle, thus we get,
\[AB = BC = CA\]
Let us take, \[AB = BC = CA = a\]
Also, \[\vartriangle BDE\] is a equilateral triangle, thus we get,
\[BD = DE = EB\].
Let us take, \[BD = DE = EB = b\]
The area of the equilateral triangle \[\vartriangle ABC\] is \[\dfrac{{\sqrt 3 }}{4}{a^2}\]
The area of the equilateral triangle \[\vartriangle BDE\] is \[\dfrac{{\sqrt 3 }}{4}{b^2}\]
Also given that, \[BD = BC\]
Therefore, \[a = b\]
Therefore, the ratio of areas of the equilateral triangles \[\vartriangle ABC\] and \[\vartriangle BDE\]is
\[ \Rightarrow \dfrac{{\dfrac{{\sqrt 3 }}{4}{a^2}}}{{\dfrac{{\sqrt 3 }}{4}{b^2}}}\]
By using \[a = b\] we get,
\[ \Rightarrow \dfrac{{\dfrac{{\sqrt 3 }}{4}{b^2}}}{{\dfrac{{\sqrt 3 }}{4}{b^2}}}\]
Simplifying we get,
\[ \Rightarrow \dfrac{1}{1}\]
Hence,
\[ \Rightarrow 1:1\]

\[\therefore \] The ratio of areas of the equilateral triangles \[\vartriangle ABC\] and
\[\vartriangle BDE\] is \[1:1\].

Note: In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each \[60^\circ \] .