Question

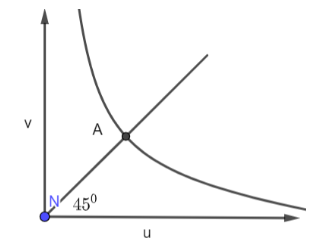
Variation of $v$ and $u$ for a spherical mirror is shown. The curve is a hyperbola. A straight line of unit slope intersects the curve at $A$. If the focal length of the mirror is 20 cm, the coordinates of point $A$ are ?

A. 20 cm, 10 cm
B. 40 cm, 40 cm
C. 40 cm, 20 cm
D. 20 cm, 20 cm

Answer 1

Hint: Since the straight line intersects the hyperbola, the point A has to satisfy both the curves. This means that the coordinates of point A can be taken as (v, u) and it will satisfy the relation $\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$ where $f$ is the focal length of the mirror, $u$ is the object distance from the mirror and $v$ is the image distance from the mirror. We will calculate the slope of the line from which we shall obtain a relation between the object distance and the image distance. Substituting in the formula for the focal length will give us the coordinates of point A.

Complete step by step answer:
The graph is plotted between v (image distance) and u (object distance) for a spherical mirror. Let the coordinates of A be (v, u).

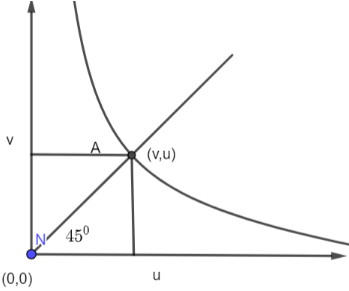
The slope of the graph is given by $m = \dfrac{{v - 0}}{{u - 0}}$
$ \Rightarrow m = \dfrac{v}{u}$
It is given in the question that the slope of the line intersecting the hyperbola is 1.
Hence, $m = 1$
So, $m = \dfrac{v}{u} = 1$
This can be rewritten as
$v = u$
For the spherical mirrors, the relation between the focal length, image distance and object distance is given by
$\dfrac{1}{f} = \dfrac{1}{v} + \dfrac{1}{u}$
where $f$ is the focal length of the mirror, $u$ is the object distance from the mirror and $v$ is the image distance from the mirror.

Since $v = u$ , the above formula reduces to $\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{u}$
This can be further simplified as $\dfrac{1}{f} = \dfrac{2}{u}$
Given that the focal length of the mirror is 20 cm.
Substituting in the equation we get,
$\dfrac{1}{{20}} = \dfrac{2}{u}$
$ \Rightarrow u = 40\,cm$
Since $v = u$ , $v = 40\,cm$
So, the coordinates of point A are 40 cm, 40 cm.

Hence, option B is the correct answer.

Note: We must take a proper note of the sign conventions while dealing with mirrors. While substituting values in the formulas, a good care of the signs must be taken. Else we will get wrong results. In this question, a positive unit slope means that the image and object both are at the same distance from the mirror and at the same side also. The size of the image is exactly the same as that of the object.