Question

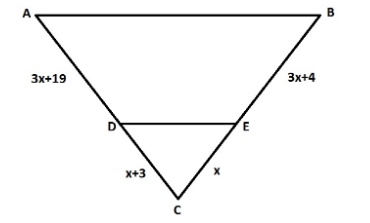
What values of $ x $ will make \[DE\parallel AB\] in the given figure?

Answer 1

Hint: We are given different dimensions in terms of $ x $ as shown in the figure. We need to make an equation and then solve it to find $ x $ . The condition given is the value of $ x $ must make \[DE\parallel AB\] . For finding this particular value of $ x $ , we will use the converse of basic proportionality theorem and make a quadratic equation.

Complete step-by-step answer:
We know that the converse of basic proportionality theorem states that If a line divides any two sides of the triangle in the same ratio, then the line must be parallel to the third side.
Here, line DE divides two sides AC and BC of the given triangle. Now, as per the converse of basic proportionality theorem, \[DE\parallel AB\] when line DE divides both the sides of the triangle in the same ratio which means that
 $ \dfrac{{CD}}{{DA}} = \dfrac{{CE}}{{EB}} $
It is given in the figure that
 $
  CD = x + 3 \\
  DA = 3x + 19 \\
  CE = x \\
  EB = 3x + 4 \;
  $
Putting these values, we get
 $
  \dfrac{{CD}}{{DA}} = \dfrac{{CE}}{{EB}} \\
   \Rightarrow \dfrac{{x + 3}}{{3x + 19}} = \dfrac{x}{{3x + 4}} \\
   \Rightarrow \left( {x + 3} \right)\left( {3x + 4} \right) = x\left( {3x + 19} \right) \\
   \Rightarrow 3{x^2} + 13x + 12 = 3{x^2} + 19x \\
   \Rightarrow 6x - 12 = 0 \\
   \Rightarrow x = \dfrac{{12}}{6} \\
   \Rightarrow x = 2 \;
  $
Thus, when the value of $ x $ is 2, \[DE\parallel AB\] in the given figure.
So, the correct answer is “x=2”.

Note: Here, we have used the converse of the basic proportionality theorem which states that if a line divides any two sides of the triangle in the same ratio, then the line must be parallel to the third side to find the required value of $ x $ . We should also remember that if a line is drawn parallel to any one side of the triangle, it divides the other two sides of the triangle in the same ratio. This is called the basic proportionality theorem.