Question

Using theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side

Answer 1

Hint: Since the line intersects at the mid-points of the two sides, their ratio will be proportional to each other and according to theorem 6.2. if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.

Complete step-by-step answer:
Let us consider a triangle ABC having sides AB, AC and BC where X and Y are the mid points of side AB and AC respectively and a line joins the points X and Y. Now we have to prove that the line XY is parallel to BC.

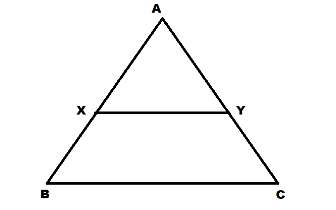
To solve the above question first we have to know the theorem 6.2 and Basic Proportionality theorem which states as below
Theorem 6.2: If a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side of the triangle.
Basic Proportionality Theorem (can be abbreviated as BPT) states that, if a line is parallel to a side of a triangle which intersects the other sides into two distinct points, then the line divides those sides in proportion.
Now, since X and Y are the mid points of AB and AC respectively, AX=XB and AY=YC.
Therefore, \[\dfrac{{AX}}{{XB}} = 1\] and \[\dfrac{{AY}}{{YC}} = 1\]
So, \[\dfrac{{AX}}{{XB}} = \dfrac{{AY}}{{YC}} = 1\]
Hence, \[\dfrac{{AX}}{{XB}} = \dfrac{{AY}}{{YC}}\]
Hence, from the Basic Proportionality Theorem we can conclude that XY is parallel to BC.

Note: If we see the above stated two theorems, we will see that both are the same only the condition and the conclusion getting vice versa in both the cases. So, if we understand and remember any one theorem we can easily remember the other one and can accordingly solve similar types of questions.