Question

Using the method of integration, find the area of the region bounded by the lines $3x-2y+1=0,2x+3y-21=0$ and $x-5y+9=0$.

Answer 1

- Hint: In this question, we have been given the equation of three lines and we have to find the area of the region bounded by these lines. For that, we will find the point of intersection by solving the three equations for x, y and z using the elimination method. Then we will find the area by computing the integral of the three equations along with the limits according to the point of intersections.

Complete step-by-step solution
We have been provided with the equation of three lines. So, basically they represent three linear equations. Let us number them as,
$\begin{align}
  & 3x-2y+1=0-(1) \\
 & 2x+3y-21=0-(2) \\
 & x-5y+9=0-(3) \\
\end{align}$
Now we will find the point of intersection of lines represented by equations (1) and (2). We will multiply equation (1) with 2 and equation (2) with 3 in order to eliminate variable x.
$\begin{align}
  & 2\times (3x-2y+1=0) \\
 & 3\times (2x+3y-21=0) \\
\end{align}$
Now when we solve these equations, we will get
$\begin{align}
  & 6x-4y+2=0 \\
 & 6x+9y-63=0 \\
\end{align}$
Now we will subtract these equations and we will get $13y=65$
So, we will get the value of y as y=5.
Now putting the value of y=5 in equation (1), we will get
$\begin{align}
  & 6x-4(5)+2=0 \\
 & 6x=18 \\
\end{align}$
We will get the value of x=3.
So, the point of intersection of (1) and (2) is (3,5).
Now we will find the point of intersection for lines represented by equations (2) and (3). We will multiply equation (3) with 2 in order to eliminate variable x.
$\begin{align}
  & 1\times (2x+3y-21=0) \\
 & 2\times (x-5y+9=0) \\
\end{align}$
Now when we solve these equations, we will get
$\begin{align}
  & 2x+3y-21=0 \\
 & 2x-10y+18=0 \\
\end{align}$
Now we will subtract these two equations and we will get $13y=39$.
After solving this, we will get y as y=3.
Now putting the value of y=3 in the equation (2), we will get
$\begin{align}
  & 2x+3(3)-21=0 \\
 & 2x=12 \\
\end{align}$
We will get the value of x=6.
So, the point of intersection of (2) and (3) is (3,6).
Now we will find the point of intersection for lines represented by equations (1) and (3). We will multiply equation (3) with 3 in order to eliminate variable x.
$\begin{align}
  & 1\times (3x-2y+1=0) \\
 & 3\times (x-5y+9=0) \\
\end{align}$
Now when we solve these equations, we will get
$\begin{align}
  & 3x-2y+1=0 \\
 & 3x-15y+27=0 \\
\end{align}$
Now we will subtract these two equations and we will get $13y=26$.
We will get the value of y as y=2.
Now putting the value of y=2 in the equation (1), we will get
$\begin{align}
  & 3x-2(2)+1=0 \\
 & 3x=3 \\
\end{align}$
We will get the value of x=1.
So, the point of intersection of (1) and (3) is (1,2).
Now with the help of these intersection points, we will draw these lines on the graph,

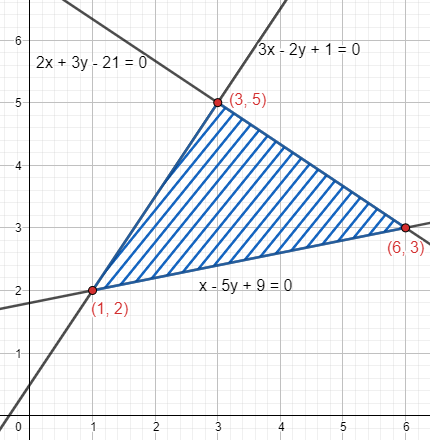
Now we will find the area of the region for which we need to find the integration of these lines according to the limits,
$\int\limits_{1}^{3}{\dfrac{3x+1}{2}}dx+\int\limits_{3}^{6}{\dfrac{-2x+21}{3}}dx-\int\limits_{1}^{6}{\dfrac{x+9}{5}dx}$
Now simplifying the above equation, we will get
$\dfrac{3}{2}\int\limits_{1}^{3}{xdx+\dfrac{1}{2}\int\limits_{1}^{3}{dx}-\dfrac{2}{3}}\int\limits_{3}^{6}{xdx}+7\int\limits_{3}^{6}{dx}-\dfrac{1}{5}\int\limits_{1}^{6}{xdx}-\dfrac{9}{5}\int\limits_{1}^{6}{dx}$
Now integrating the above equation, we will get
$\dfrac{3}{2}{{\left[ \dfrac{{{x}^{2}}}{2} \right]}^{3}}_{1}+\dfrac{1}{2}{{\left[ x \right]}^{3}}_{1}-\dfrac{2}{3}{{\left[ \dfrac{{{x}^{2}}}{2} \right]}^{6}}_{3}+7{{\left[ x \right]}^{6}}_{3}-\dfrac{1}{5}{{\left[ \dfrac{{{x}^{2}}}{2} \right]}^{6}}_{1}-\dfrac{9}{5}{{\left[ x \right]}^{6}}_{1}$
Now putting the limits, we will get
$\dfrac{3}{4}\left( 9-1 \right)+\dfrac{1}{2}(3-1)-\dfrac{2}{6}(36-9)+7(6-3)-\dfrac{1}{10}(36-1)-\dfrac{9}{5}(6-1)$
Now solving the equations further, we will get
$6+1-9+21-\dfrac{7}{2}-9$
Solving it further we will get the area of the region: $\dfrac{13}{2}$ .
So, this is the solution for this question.

Note: In this question we should be a little bit cautious while putting the limits as chances of mistakes over there is a lot higher. Also do find the points of intersection for all the equations differently by using elimination and substitution method. Don’t forget to mark the region whose area needs to be calculated.