Question

Using ruler and compasses only, construct a parallelogram ABCD using the following data:
AB = 6 cm, AD = 3 cm and $\angle DAB=45{}^\circ $. If the bisector of $\angle DAB$ a meets BC at P, prove that $\angle APB$ is right angle.

Answer 1

Hint: For solving this problem, we adopted a step-by-step procedure for the construction of a parallelogram by using a ruler and compass. In the second part, we use the property of the co-interior angles of a parallelogram and the property of the sum of all the angles of the triangle to prove the required part.

Complete step-by-step solution:
For the construction of parallelogram ABCD:
First of all, by using a ruler, we are going to draw a line segment AB of length 6 cm.

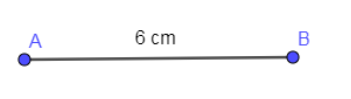
Now using a compass, we are going to draw a perpendicular on this line segment AB by extending line segment AB and then we are going to mark a point P above the line segment AB.

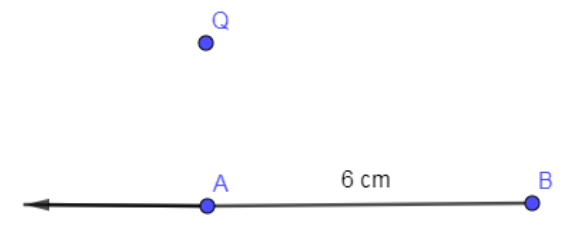
Now, from Q we are making two arcs on the line AB as follows with the same radius as follows:

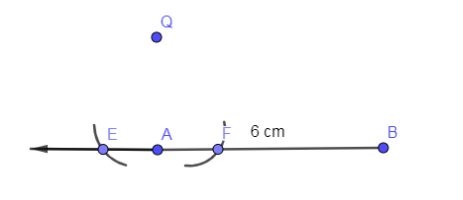
Now, with the same radius, place the needle on the point E, draw an arc below line AB and place the needle on the vertex F and draw an arc which is cutting the first arc.

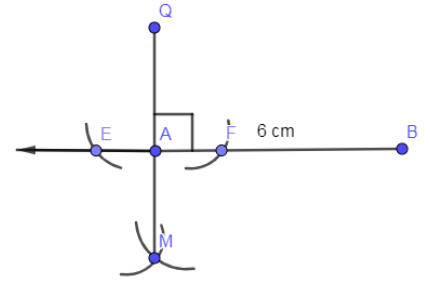
In the above diagram, we have marked the intersection point of the arcs as M and then joined Q and M and hence, we got the perpendicular AQ on AB.
After that, we will draw an angle bisector of angle BAQ as follows:

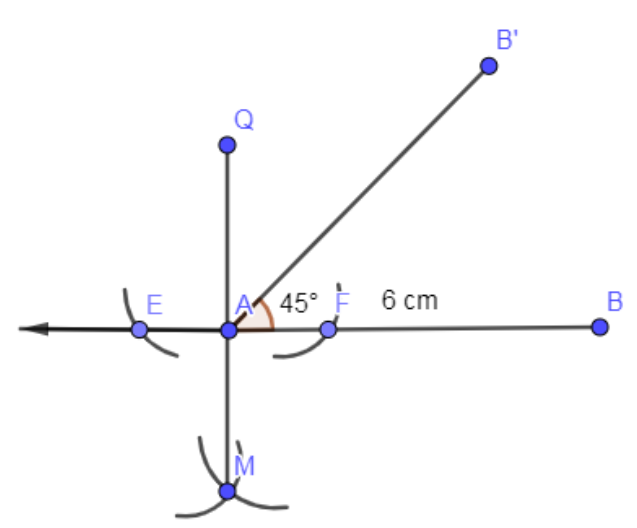
Now, open the compass of radius 3 cm and place a needle on the point A and mark an arc on AB’.

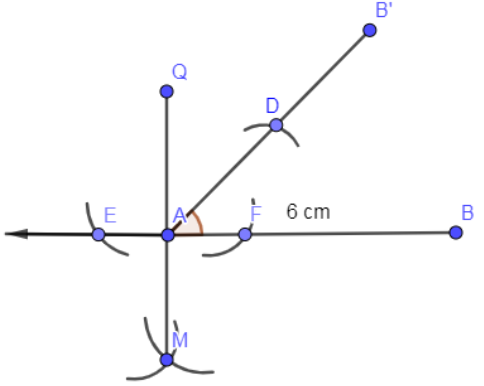
Now, place the needle on the point D and with radius 6 cm, mark an arc and also place the needle of the compass on vertex B and mark an arc of radius 3 cm.

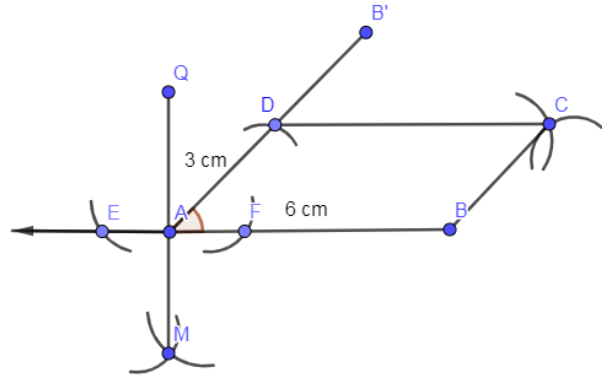
Now, we are going to draw the angle bisector of angle BAD which meets DC at P.

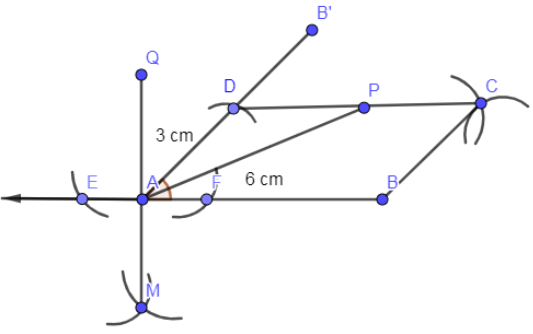
Now, we are going to join A with P.

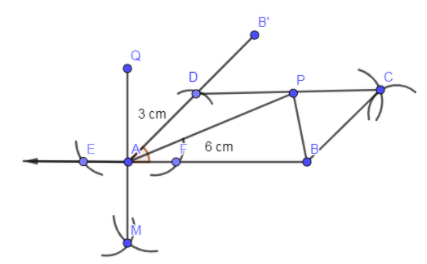
Now proceeding for proving $\angle APB$ is right angle:
In a parallelogram, the sum of co interior angles is 180. Hence,
$\begin{align}
  & \angle BAD+\angle ABC=180{}^\circ \\
 &\Rightarrow 45{}^\circ +\angle ABC=180{}^\circ \\
 &\Rightarrow \angle ABC=\left( 180-45 \right){}^\circ \\
 &\Rightarrow \angle ABC=135{}^\circ \\
\end{align}$
Also, it is given that $\angle BAP$ is the bisector of $\angle BAD$ and $\angle ABP$ is the bisector of $\angle ABC$ because P is the midpoint of DC.
As we know that the sum of all the angles of a triangle is equivalent to 180 degrees. So, in triangle APB:
$\begin{align}
  & \angle APB+\angle PBA+\angle BAP=180{}^\circ \\
 &\Rightarrow \angle APB+22.5{}^\circ +67.5{}^\circ =180{}^\circ \\
 &\Rightarrow \angle APB=\left( 180-22.5-67.5 \right){}^\circ \\
 &\Rightarrow \angle APB=90{}^\circ \\
\end{align}$
Therefore, $\angle APB$ is a right angle.

Note: For drawing an angle of 45-degree, a student must first draw 90 degrees and then take the bisector of it. Once the angle is drawn then you must mark an arc of 3cm and erase the rest part of the ray AX to obtain AD. Sufficiently long arcs should be drawn to find the intersection point C.