Question

Using monochromatic light of wavelength$\lambda $, an experiment set up the Young’s double slit experiment in three ways as shown.

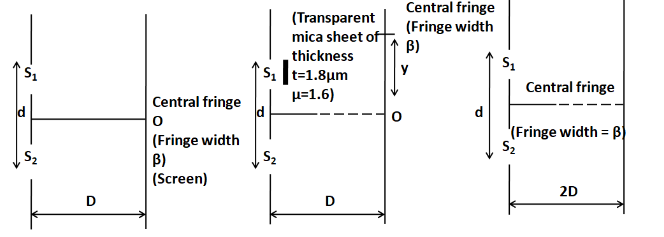
If she observes that $y = \beta $, the wavelength of light used is:
(A) $520nm$
(B) $540nm$
(C) $560nm$
(D) $580nm$

Answer 1

Hint : To solve this question, we need to apply the formula of the path difference and the fringe width in the case of Young’s double slit experiment. Modifying these expressions according to the three different situations given, we will get the final answer.

Formula Used: The formulae used in solving this question are given by:
$w = \dfrac{{\lambda D}}{d}$, here $w$ is the fringe width, $\lambda $ is the wavelength of the light used,$D$is the distance of the screen from the slits, and$d$is the distance between the two slits.
$x = t\left( {\mu - 1} \right)$, here $x$ is the path difference offered by a transparent material of thickness $t$ and having a refractive index of $\mu $.

Complete step by step answer
There are three set ups of the Young’s double slit experiment. The first is the general set up, in which all the conditions are simple. In the second set up, all the conditions are the same, except that we have a mica sheet in front of the slit S1 due to which the fringe pattern shifts upwards. In the third setup, only the distance between the slit and the screen is doubled.
Now, we know that the fringe width in a Young’s double slit experiment is given by
$w = \dfrac{{\lambda D}}{d}$ (1)
Now, for the second case we have a transparent mica sheet of refractive index $\mu = 1.6$ and thickness $t = 1.8\mu m$.

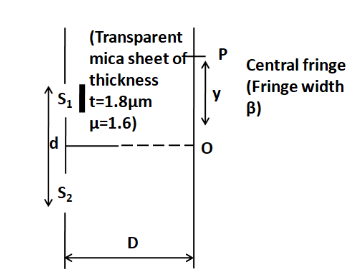
This sheet will affect the path difference between the rays originating from the slits S1 and S2. We know that the extra path difference offered by a transparent medium is given by
$x = t\left( {\mu - 1} \right)$
So, the path difference between the rays from S1 and S2 at the point P is given by
$PD = {S_2}P - \;\left( {{S_1}\;P + x} \right)$
\[PD = {S_2}P - {S_1}\;P - t\left( {\mu - 1} \right)\]
Here ${S_2}P - {S_1}\;P = \dfrac{{yd}}{D}$, the original path difference. So, we get
\[PD = \dfrac{{yd}}{D} - t\left( {\mu - 1} \right)\]
For the central bright fringe, the path difference must be zero, that is
\[\dfrac{{yd}}{D} - t\left( {\mu - 1} \right) = 0\]
\[\dfrac{{yd}}{D} = t\left( {\mu - 1} \right)\]
So the position of the central bright fringe is given by
\[{y_0} = \dfrac{{t\left( {\mu - 1} \right)D}}{d}\]
The next bright fringe will occur at twice this distance. So
\[{y_1} = \dfrac{{2t\left( {\mu - 1} \right)D}}{d}\]
Now, as the fringe width is the distance between two consecutive bright fringes, so we have
$w = {y_1} - {y_0}$
\[w = \dfrac{{2t\left( {\mu - 1} \right)D}}{d} - \dfrac{{t\left( {\mu - 1} \right)D}}{d}\]
According to the question the fringe width in this case is $w = \beta $. So we have
\[\beta = \dfrac{{t\left( {\mu - 1} \right)D}}{d}\] (2)
Finally, in the last case we have distance between the slits and the screen is $2D$.
So, the fringe width in this case from (1) is given by
$w = \dfrac{{\lambda \left( {2D} \right)}}{d}$
$w = \dfrac{{2\lambda D}}{d}$
According to the question, we have$w = \beta $. So we have
$\beta = \dfrac{{2\lambda D}}{d}$ (3)
From (2) and (3) we get
$\dfrac{{2\lambda D}}{d} = \dfrac{{t\left( {\mu - 1} \right)D}}{d}$
So we get the wavelength of the light as
$\lambda = \dfrac{{t\left( {\mu - 1} \right)}}{2}$
According to the question, we have $\mu = 1.6$ and $t = 1.8\mu m$. Substituting these, we get
$\lambda = \dfrac{{1.8\left( {1.6 - 1} \right)}}{2}\mu m$
On solving we get
$\lambda = 0.54\mu m$
Converting into nanometers, we get
$\lambda = 540nm$
Hence, the correct answer is option B.

Note
Do not mix the three cases given in the question. Deal with each case separately, write the results for it, and then move ahead for the next case. Otherwise, there are high chances of committing mistakes in these types of questions.